AES Encryption Algorithm

Federal Information
Processing Standards Publication 197

November 26, 2001

Announcing the

ADVANCED ENCRYPTION STANDARD (AES)

Federal Information Processing Standards Publications (FIPS PUBS) are issued by the National Institute of Standards and Technology (NIST) after approval by the Secretary of Commerce pursuant to Section 5131 of the Information Technology Management Reform Act of 1996 (Public Law 104-106) and the Computer Security Act of 1987 (Public Law 100-235).

1. Name of Standard. Advanced Encryption Standard (AES) (FIPS PUB 197).

2. Category of Standard. Computer Security Standard, Cryptography.

3. Explanation. The Advanced Encryption Standard (AES) specifies a FIPS-approved cryptographic algorithm that can be used to protect electronic data. The AES algorithm is a symmetric block cipher that can encrypt (encipher) and decrypt (decipher) information. Encryption converts data to an unintelligible form called ciphertext; decrypting the ciphertext converts the data back into its original form, called plaintext.

The AES algorithm is capable of using cryptographic keys of 128, 192, and 256 bits to encrypt and decrypt data in blocks of 128 bits.

4. Approving Authority. Secretary of Commerce.

5. Maintenance Agency. Department of Commerce, National Institute of Standards and Technology, Information Technology Laboratory (ITL).

6. Applicability. This standard may be used by Federal departments and agencies when an agency determines that sensitive (unclassified) information (as defined in P. L. 100-235) requires cryptographic protection.

Other FIPS-approved cryptographic algorithms may be used in addition to, or in lieu of, this standard. Federal agencies or departments that use cryptographic devices for protecting classified information can use those devices for protecting sensitive (unclassified) information in lieu of this standard.

In addition, this standard may be adopted and used by non-Federal Government organizations. Such use is encouraged when it provides the desired security for commercial and private organizations.

7. Specifications. Federal Information Processing Standard (FIPS) 197, Advanced Encryption Standard (AES) (affixed).

8. Implementations. The algorithm specified in this standard may be implemented in software, firmware, hardware, or any combination thereof. The specific implementation may depend on several factors such as the application, the environment, the technology used, etc. The algorithm shall be used in conjunction with a FIPS approved or NIST recommended mode of operation. Object Identifiers (OIDs) and any associated parameters for AES used in these modes are available at the Computer Security Objects Register (CSOR), located at http://csrc.nist.gov/csor/ [2].

Implementations of the algorithm that are tested by an accredited laboratory and validated will be considered as complying with this standard. Since cryptographic security depends on many factors besides the correct implementation of an encryption algorithm, Federal Government employees, and others, should also refer to NIST Special Publication 800-21, Guideline for Implementing Cryptography in the Federal Government, for additional information and guidance (NIST SP 800-21 is available at http://csrc.nist.gov/publications/).

9. Implementation Schedule. This standard becomes effective on May 26, 2002.

10. Patents. Implementations of the algorithm specified in this standard may be covered by U.S. and foreign patents.

11. Export Control. Certain cryptographic devices and technical data regarding them are subject to Federal export controls. Exports of cryptographic modules implementing this standard and technical data regarding them must comply with these Federal regulations and be licensed by the Bureau of Export Administration of the U.S. Department of Commerce. Applicable Federal government export controls are specified in Title 15, Code of Federal Regulations (CFR) Part 740.17; Title 15, CFR Part 742; and Title 15, CFR Part 774, Category 5, Part 2.

12. Qualifications. NIST will continue to follow developments in the analysis of the AES algorithm. As with its other cryptographic algorithm standards, NIST will formally reevaluate this standard every five years.

Both this standard and possible threats reducing the security provided through the use of this standard will undergo review by NIST as appropriate, taking into account newly available analysis and technology. In addition, the awareness of any breakthrough in technology or any mathematical weakness of the algorithm will cause NIST to reevaluate this standard and provide necessary revisions.

13. Waiver Procedure. Under certain exceptional circumstances, the heads of Federal agencies, or their delegates, may approve waivers to Federal Information Processing Standards (FIPS). The heads of such agencies may redelegate such authority only to a senior official designated pursuant to Section 3506(b) of Title 44, U.S. Code. Waivers shall be granted only when compliance with this standard would

a. adversely affect the accomplishment of the mission of an operator of Federal computer system or

b. cause a major adverse financial impact on the operator that is not offset by government-wide savings.

Agency heads may act upon a written waiver request containing the information detailed above. Agency heads may also act without a written waiver request when they determine that conditions for meeting the standard cannot be met. Agency heads may approve waivers only by a written decision that explains the basis on which the agency head made the required finding(s). A copy of each such decision, with procurement sensitive or classified portions clearly identified, shall be sent to: National Institute of Standards and Technology; ATTN: FIPS Waiver Decision, Information Technology Laboratory, 100 Bureau Drive, Stop 8900, Gaithersburg, MD 20899-8900.

In addition, notice of each waiver granted and each delegation of authority to approve waivers shall be sent promptly to the Committee on Government Operations of the House of Representatives and the Committee on Government Affairs of the Senate and shall be published promptly in the Federal Register.

When the determination on a waiver applies to the procurement of equipment and/or services, a notice of the waiver determination must be published in the Commerce Business Daily as a part of the notice of solicitation for offers of an acquisition or, if the waiver determination is made after that notice is published, by amendment to such notice.

A copy of the waiver, any supporting documents, the document approving the waiver and any supporting and accompanying documents, with such deletions as the agency is authorized and decides to make under Section 552(b) of Title 5, U.S. Code, shall be part of the procurement documentation and retained by the agency.

14. Where to obtain copies. This publication is available electronically by accessing http://csrc.nist.gov/publications/. A list of other available computer security publications, including ordering information, can be obtained from NIST Publications List 91, which is available at the same web site. Alternatively, copies of NIST computer security publications are available from: National Technical Information Service (NTIS), 5285 Port Royal Road, Springfield, VA 22161.

Federal Information
Processing Standards Publication 197

November 26, 2001

Specification for the

ADVANCED ENCRYPTION STANDARD (AES)

Table of Contents

1. INTRODUCTION

2. DEFINITIONS

2.1 GLOSSARY OF TERMS AND ACRONYMS

2.2 ALGORITHM PARAMETERS, SYMBOLS, AND FUNCTIONS

3. NOTATION AND CONVENTIONS

3.1 INPUTS AND OUTPUTS

3.2 BYTES

3.3 ARRAYS OF BYTES

3.4 THE STATE

3.5 THE STATE AS AN ARRAY OF COLUMNS

4. MATHEMATICAL PRELIMINARIES

4.1 ADDITION

4.2 MULTIPLICATION

4.2.1 Multiplication by x

4.3 POLYNOMIALS WITH COEFFICIENTS IN GF(28)

5. ALGORITHM SPECIFICATION

5.1 CIPHER

5.1.1 SubBytes()Transformation

5.1.2 ShiftRows() Transformation

5.1.3 MixColumns() Transformation

5.1.4 AddRoundKey() Transformation

5.2 KEY EXPANSION

5.3 INVERSE CIPHER

5.3.1 InvShiftRows() Transformation

5.3.2 InvSubBytes() Transformation

5.3.3 InvMixColumns() Transformation

5.3.4 Inverse of the AddRoundKey() Transformation

5.3.5 Equivalent Inverse Cipher

6. IMPLEMENTATION ISSUES

6.1 KEY LENGTH REQUIREMENTS

6.2 KEYING RESTRICTIONS

6.3 PARAMETERIZATION OF KEY LENGTH, BLOCK SIZE, AND ROUND NUMBER

6.4 IMPLEMENTATION SUGGESTIONS REGARDING VARIOUS PLATFORMS

APPENDIX A - KEY EXPANSION EXAMPLES

A.1 EXPANSION OF A 128-BIT CIPHER KEY

A.2 EXPANSION OF A 192-BIT CIPHER KEY

A.3 EXPANSION OF A 256-BIT CIPHER KEY

APPENDIX B û CIPHER EXAMPLE

APPENDIX C û EXAMPLE VECTORS

C.1 AES-128 (NK=4, NR=10)

C.2 AES-192 (NK=6, NR=12)

C.3 AES-256 (NK=8, NR=14)

APPENDIX D - REFERENCES

Table of Figures

Figure 1. Hexadecimal representation of bit patterns.

Figure 2. Indices for Bytes and Bits.

Figure 3. State array input and output.

Figure 4. Key-Block-Round Combinations.

Figure 5. Pseudo Code for the Cipher.

Figure 6. SubBytes() applies the S-box to each byte of the State.

Figure 7. S-box: substitution values for the byte xy (in hexadecimal format).

Figure 8. ShiftRows() cyclically shifts the last three rows in the State.

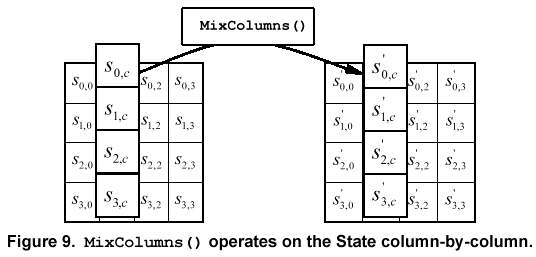
Figure 9. MixColumns() operates on the State column-by-column.

Figure 10. AddRoundKey() XORs each column of the State with a word from the key schedule.

Figure 11. Pseudo Code for Key Expansion.

Figure 12. Pseudo Code for the Inverse Cipher.

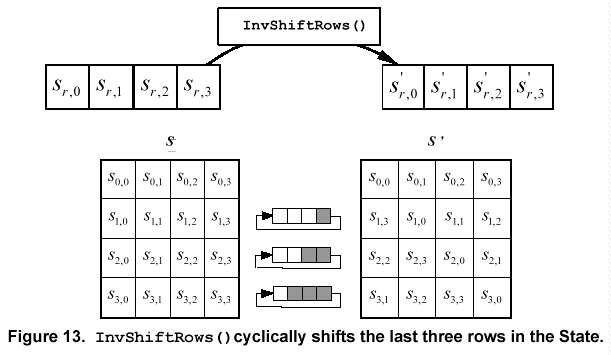
Figure 13. InvShiftRows() cyclically shifts the last three rows in the State.

Figure 14. Inverse S-box: substitution values for the byte xy (in hexadecimal format).

Figure 15. Pseudo Code for the Equivalent Inverse Cipher.

1. Introduction

This standard specifies the Rijndael algorithm ([3] and [4]), a symmetric block cipher that can process data blocks of 128 bits, using cipher keys with lengths of 128, 192, and 256 bits. Rijndael was designed to handle additional block sizes and key lengths, however they are not adopted in this standard.

Throughout the remainder of this standard, the algorithm specified herein will be referred to as ôthe AES algorithm.ö The algorithm may be used with the three different key lengths indicated above, and therefore these different ôflavorsö may be referred to as ôAES-128ö, ôAES-192ö, and ôAES-256ö.

This specification includes the following sections:

2. Definitions of terms, acronyms, and algorithm parameters, symbols, and functions;

3. Notation and conventions used in the algorithm specification, including the ordering and numbering of bits, bytes, and words;

4. Mathematical properties that are useful in understanding the algorithm;

5. Algorithm specification, covering the key expansion, encryption, and decryption routines;

6. Implementation issues, such as key length support, keying restrictions, and additional block/key/round sizes.

The standard concludes with several appendices that include step-by-step examples for Key Expansion and the Cipher, example vectors for the Cipher and Inverse Cipher, and a list of references.

2. Definitions

2.1 Glossary of Terms and Acronyms

The following definitions are used throughout this standard:

AES á áAdvanced Encryption Standard

Affine á áA transformation consisting of multiplication by a matrix followed by Transformation the addition of a vector.

Array á áAn enumerated collection of identical entities (e.g., an array of bytes).

Bit á áA binary digit having a value of 0 or 1.

Block á áSequence of binary bits that comprise the input, output, State, and Round Key. The length of a sequence is the number of bits it contains. Blocks are also interpreted as arrays of bytes.

Byte á áA group of eight bits that is treated either as a single entity or as an array of 8 individual bits.

Cipher á áSeries of transformations that converts plaintext to ciphertext using the Cipher Key.

Cipher Key á áSecret, cryptographic key that is used by the Key Expansion routine to generate a set of Round Keys; can be pictured as a rectangular array of bytes, having four rows and Nk columns.

Ciphertext á áData output from the Cipher or input to the Inverse Cipher.

Inverse Cipher á áSeries of transformations that converts ciphertext to plaintext using the Cipher Key.

Key Expansion á áRoutine used to generate a series of Round Keys from the Cipher Key.

Plaintext á áData input to the Cipher or output from the Inverse Cipher.

Rijndael á áCryptographic algorithm specified in this Advanced Encryption Standard (AES).

Round Key á áRound keys are values derived from the Cipher Key using the Key Expansion routine; they are applied to the State in the Cipher and Inverse Cipher.

State á áIntermediate Cipher result that can be pictured as a rectangular array of bytes, having four rows and Nb columns.

S-box á áNon-linear substitution table used in several byte substitution transformations and in the Key Expansion routine to perform a one-for-one substitution of a byte value.

Word á áA group of 32 bits that is treated either as a single entity or as an array of 4 bytes.

2.2 Algorithm Parameters, Symbols, and Functions

The following algorithm parameters, symbols, and functions are used throughout this standard:

AddRoundKey() Transformation in the Cipher and Inverse Cipher in which a Round Key is added to the State using an XOR operation. The length of a Round Key equals the size of the State (i.e., for Nb = 4, the Round Key length equals 128 bits/16 bytes).

InvMixColumns() áTransformation in the Inverse Cipher that is the inverse of MixColumns().

InvShiftRows() á Transformation in the Inverse Cipher that is the inverse of ShiftRows().

InvSubBytes() á Transformation in the Inverse Cipher that is the inverse of SubBytes().

K á Cipher Key.

MixColumns() á Transformation in the Cipher that takes all of the columns of the State and mixes their data (independently of one another) to produce new columns.

Nb á Number of columns (32-bit words) comprising the State. For this standard, Nb = 4. (Also see Sec. 6.3.)

Nk á Number of 32-bit words comprising the Cipher Key. For this standard, Nk = 4, 6, or 8. (Also see Sec. 6.3.)

Nr á Number of rounds, which is a function of Nk and Nb (which is fixed). For this standard, Nr = 10, 12, or 14. (Also see Sec. 6.3.)

Rcon[] á The round constant word array.

RotWord() á Function used in the Key Expansion routine that takes a four-byte word and performs a cyclic permutation.

ShiftRows() áTransformation in the Cipher that processes the State by cyclically shifting the last three rows of the State by different offsets.

SubBytes() áTransformation in the Cipher that processes the State using a non-linear byte substitution table (S-box) that operates on each of the State bytes independently.

SubWord() á Function used in the Key Expansion routine that takes a four-byte input word and applies an S-box to each of the four bytes to produce an output word.

XOR á Exclusive-OR operation.

áExclusive-OR operation.

Multiplication of two polynomials (each with degree < 4) modulo x4 + 1.

á Finite field multiplication.

3. Notation and Conventions

3.1 Inputs and Outputs

The input and output for the AES algorithm each consist of sequences of 128 bits (digits with values of 0 or 1). These sequences will sometimes be referred to as blocks and the number of bits they contain will be referred to as their length. The Cipher Key for the AES algorithm is a sequence of 128, 192 or 256 bits. Other input, output and Cipher Key lengths are not permitted by this standard.

The bits within such sequences will be numbered starting at zero and ending at one less than the sequence length (block length or key length). The number i attached to a bit is known as its index and will be in one of the ranges 0 < i < 128, 0 < i < 192 or 0 < i < 256 depending on the block length and key length (specified above).

3.2 Bytes

The basic unit for processing in the AES algorithm is a byte, a sequence of eight bits treated as a single entity. The input, output and Cipher Key bit sequences described in Sec. 3.1 are processed as arrays of bytes that are formed by dividing these sequences into groups of eight contiguous bits to form arrays of bytes (see Sec. 3.3). For an input, output or Cipher Key denoted by a, the bytes in the resulting array will be referenced using one of the two forms, an or a[n], where n will be in one of the following ranges:

Key length = 128 bits, 0 < n < 16; Block length = 128 bits, 0 < n < 16;

Key length = 192 bits, 0 < n < 24;

Key length = 256 bits, 0 < n < 32.

All byte values in the AES algorithm will be presented as the concatenation of its individual bit values (0 or 1) between braces in the order {b7, b6, b5, b4, b3, b2, b1, b0}. These bytes are interpreted as finite field elements using a polynomial representation:

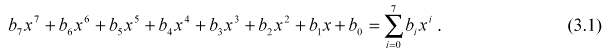
For example, {01100011} identifies the specific finite field element x6 + x5 + x +1.

It is also convenient to denote byte values using hexadecimal notation with each of two groups of four bits being denoted by a single character as in Fig. 1.

Figure 1. Hexadecimal representation of bit patterns.

Hence the element {01100011} can be represented as {63}, where the character denoting the four-bit group containing the higher numbered bits is again to the left.

Some finite field operations involve one additional bit (b8) to the left of an 8-bit byte. Where this extra bit is present, it will appear as æ{01}Æ immediately preceding the 8-bit byte; for example, a 9-bit sequence will be presented as {01}{1b}.

3.3 Arrays of Bytes

Arrays of bytes will be represented in the following form:

a0 a1 a2 ... a15

The bytes and the bit ordering within bytes are derived from the 128-bit input sequence

input0 input1 input2 à input126 input127

as follows:

a0 = {input0 input1, ..., input7};

a1 = {input8 input9, ..., input15};

.
.
.

a15 = {input120 input121, ..., input127}.

The pattern can be extended to longer sequences (i.e., for 192- and 256-bit keys), so that, in general

an = {input8n input8n+1, ..., input8n+7}. á á á á á á á á(3.2)

Taking Sections 3.2 and 3.3 together, Fig. 2 shows how bits within each byte are numbered.

Figure 2. Indices for Bytes and Bits.

3.4 The State

Internally, the AES algorithmÆs operations are performed on a two-dimensional array of bytes called the State. The State consists of four rows of bytes, each containing Nb bytes, where Nb is the block length divided by 32. In the State array denoted by the symbol s, each individual byte has two indices, with its row number r in the range 0 < r < 4 and its column number c in the range 0 < c < Nb. This allows an individual byte of the State to be referred to as either sr,c or s[r,c]. For this standard, Nb=4, i.e., 0 < c < 4 (also see Sec. 6.3).

At the start of the Cipher and Inverse Cipher described in Sec. 5, the input û the array of bytes in0, in1, à in15 û is copied into the State array as illustrated in Fig. 3. The Cipher or Inverse Cipher operations are then conducted on this State array, after which its final value is copied to the output û the array of bytes out0, out1, à out15.

Figure 3. State array input and output.

Hence, at the beginning of the Cipher or Inverse Cipher, the input array, in, is copied to the State array according to the scheme:

s[r, c] = in[r + 4c] á á á á á á for 0 < r < 4 and 0 < c < Nb á á á á á á á (3.3)

and at the end of the Cipher and Inverse Cipher, the State is copied to the output array out as follows:

out[r + 4c] = s[r, c] á á á á á á for 0 < r < 4 and 0 < c < Nb á á á á á á á (3.4)

3.5 The State as an Array of Columns

The four bytes in each column of the State array form 32-bit words, where the row number r provides an index for the four bytes within each word. The state can hence be interpreted as a one-dimensional array of 32 bit words (columns), w0 ...w3, where the column number c provides an index into this array. Hence, for the example in Fig. 3, the State can be considered as an array of four words, as follows:

w0 = s0,0 s1,0 s2,0 s3,0 á á á á á á á á á áw2 = s0,2 s1,2 s2,2 s3,2 á á á á á á á á á

w1 = s0,1 s1,1 s2,1 s3,1 á á á á á á á á á áw3 = s0,3 s1,3 s2,3 s3,3 á á á á á(3.5)

4. Mathematical Preliminaries

All bytes in the AES algorithm are interpreted as finite field elements using the notation introduced in Sec. 3.2. Finite field elements can be added and multiplied, but these operations are different from those used for numbers. The following subsections introduce the basic mathematical concepts needed for Sec. 5.

4.1 Addition

The addition of two elements in a finite field is achieved by ôaddingö the coefficients for the corresponding powers in the polynomials for the two elements. The addition is performed with the XOR operation (denoted by ) - i.e., modulo 2 - so that 1""1 = 0, 1"" 0 = 1, and 0"" 0 = 0. Consequently, subtraction of polynomials is identical to addition of polynomials.

Alternatively, addition of finite field elements can be described as the modulo 2 addition of corresponding bits in the byte. For two bytes {a7a6a5a4a3a2a1a0} and á{b7b6b5b4b3b2b1b0}, the sum is {c7c6c5c4c3c2c1c0}, where each ci = aibi (i.e., c7 = a7b7, c6 = a6b6, ... c0 = a0b0).

For example, the following expressions are equivalent to one another:

(x6 + x4 + x2 + x + 1) + (x7 + x + 1) = x7 + x6 + x4 + x2 á (polynomial notation);

{01010111}{100000111} = {11010100} á á á á á(binary notation);

{57}{83} = {d4} á á á á á á á á á á á á á á á á á á á á á á á á á á á á(hexidecimal notation).

4.2 Multiplication

In the polynomial representation, multiplication in GF(28) (denoted by ) corresponds with the multiplication of polynomials modulo an irreducible polynomial of degree 8. A polynomial is irreducible if its only divisors are one and itself. For the AES algorithm, this irreducible polynomial is

m(x) = x8 + x4 + x3 + x + 1, á á á á á á á á á á á á á á(4.1)

For example, {57}{83} = {c1}, because

and

The modular reduction by m(x) ensures that the result will be a binary polynomial of degree less than 8, and thus can be represented by a byte. Unlike addition, there is no simple operation at the byte level that corresponds to this multiplication.

The multiplication defined above is associative, and the element {01} is the multiplicative identity. For any non-zero binary polynomial b(x) of degree less than 8, the multiplicative inverse of b(x), denoted b-1(x), can be found as follows: the extended Euclidean algorithm [7] is used to compute polynomials a(x) and c(x) such that

b(x)a(x) + m(x)c(x) = 1. á á á á á á á á á á(4.2)

Hence, a(x)b(x) mod m(x) =1, which means

b-1(x) = a(x) mod m(x). á á á á á á á á á á(4.2)

Moreover, for any a(x), b(x) and c(x) in the field, it holds that

a(x)(b(x) + c(x)) = a(x)b(x) + a(x)b(x) + a(x)c(x).

It follows that the set of 256 possible byte values, with XOR used as addition and the multiplication defined as above, has the structure of the finite field GF(28).

4.2.1 Multiplication by x

Multiplying the binary polynomial defined in equation (3.1) with the polynomial x results in

b7x8 + b6x7 + b5x6 + b4x5 + b3x4 + b2x3 + b1x2 + b0x. á á á á á á á(4.4)

The result xb(x) is obtained by reducing the above result modulo m(x), as defined in equation (4.1). If b7 = 0, the result is already in reduced form. If b7 = 1, the reduction is accomplished by subtracting (i.e., XORing) the polynomial m(x). It follows that multiplication by x (i.e., {00000010} or {02}) can be implemented at the byte level as a left shift and a subsequent conditional bitwise XOR with {1b}. This operation on bytes is denoted by xtime(). Multiplication by higher powers of x can be implemented by repeated application of xtime(). By adding intermediate results, multiplication by any constant can be implemented.

For example, {57}{13} = {fe} because

{57}{02} = xtime({57}) = {ae}

{57}{04} = xtime({ae}) = {47}

{57}{08} = xtime({47}) = {8e}

{57}{10} = xtime({8e}) = {07},

thus,

{57}{13} = {57}({01}{02}{10})

á á á á á á á á á á á = {57}{ae}{07}

á á á á á á á á á á á = {fe}.

4.3 Polynomials with Coefficients in GF(28)

Four-term polynomials can be defined - with coefficients that are finite field elements - as:

a(x) = a3x3 + a2x2 + a1x + a0 á á á á á á á á á á(4.5)

which will be denoted as a word in the form [a0 , a1 , a2 , a3]. Note that the polynomials in this section behave somewhat differently than the polynomials used in the definition of finite field elements, even though both types of polynomials use the same indeterminate, x. The coefficients in this section are themselves finite field elements, i.e., bytes, instead of bits; also, the multiplication of four-term polynomials uses a different reduction polynomial, defined below. The distinction should always be clear from the context.

To illustrate the addition and multiplication operations, let

b(x) = b3x3 + b2x2 + b1x + b0 á á á á á á á á á á(4.6)

define a second four-term polynomial. Addition is performed by adding the finite field coefficients of like powers of x. This addition corresponds to an XOR operation between the corresponding bytes in each of the words û in other words, the XOR of the complete word values.

Thus, using the equations of (4.5) and (4.6),

a(x)á+áb(x) = (a3b3)x3 + (a2b2)x2 + (a1b1)x + (a0b0) á á á á á(4.7)

Multiplication is achieved in two steps. In the first step, the polynomial product c(x) = a(x)b(x) is algebraically expanded, and like powers are collected to give

c(x) = c6x6 + c5x5 + c4x4 + c3x3 + c2x2 + c1x + c0 á á á á á á á á á áá á á á(4.8)

where

The result, c(x), does not represent a four-byte word. Therefore, the second step of the multiplication is to reduce c(x) modulo a polynomial of degree 4; the result can be reduced to a polynomial of degree less than 4. For the AES algorithm, this is accomplished with the polynomial x4 + 1, so that

xi mod(x4 +1) = ximod4. á á á á á á á á á á á á á áá á á á á(4.10)

The modular product of a(x) and b(x), denoted by a(x)b(x), is given by the four-term polynomial d(x), defined as follows:

d(x) = d3x3 + d2x2 + d1x + d0 á á á á á á á á á áá á á á á(4.11)

with

d0 = (a0b0)(a3b1)(a2b2)(a1b3)

d01= (a1b0)(a0b1)(a3b2)(a2b3) á á á á á á á á á á á(4.12)

d2 = (a2b0)(a1b1)(a0b2)(a3b3)

d3 = (a3b0)(a2b1)(a1b2)(a0b3)

When a(x) is a fixed polynomial, the operation defined in equation (4.11) can be written in matrix form as:

Because x4 +1 is not an irreducible polynomial over GF(28), multiplication by a fixed four-term polynomial is not necessarily invertible. However, the AES algorithm specifies a fixed four-term polynomial that does have an inverse (see Sec. 5.1.3 and Sec. 5.3.3):

a(x) = {03}x3 + {01}x2 + {01}x + {02} á á á á á á á á á (4.14)

a-1(x) = {0b}x3 + {0d}x2 + {09}x + {0e}. á á á á á á á (4.15)

Another polynomial used in the AES algorithm (see the RotWord() function in Sec. 5.2) has a0 = a1 = a2 = {00} and a3 = {01}, which is the polynomial x3 . Inspection of equation (4.13) above will show that its effect is to form the output word by rotating bytes in the input word. This means that [b0, b1, b2, b3] is transformed into [b1, b2, b3, b0].

5. Algorithm Specification

For the AES algorithm, the length of the input block, the output block and the State is 128 bits. This is represented by Nb = 4, which reflects the number of 32-bit words (number of columns) in the State.

For the AES algorithm, the length of the Cipher Key, K, is 128, 192, or 256 bits. The key length is represented by Nk = 4, 6, or 8, which reflects the number of 32-bit words (number of columns) in the Cipher Key.

For the AES algorithm, the number of rounds to be performed during the execution of the algorithm is dependent on the key size. The number of rounds is represented by Nr, where Nr = 10 when Nk = 4, Nr = 12 when Nk = 6, and Nr = 14 when Nk = 8.

The only Key-Block-Round combinations that conform to this standard are given in Fig. 4. For implementation issues relating to the key length, block size and number of rounds, see Sec. 6.3.

Figure 4. Key-Block-Rounds Combinations.

For both its Cipher and Inverse Cipher, the AES algorithm uses a round function that is composed of four different byte-oriented transformations: 1) byte substitution using a substitution table (S-box), 2) shifting rows of the State array by different offsets, 3) mixing the data within each column of the State array, and 4) adding a Round Key to the State. These transformations (and their inverses) are described in Sec. 5.1.1-5.1.4 and 5.3.1-5.3.4.

The Cipher and Inverse Cipher are described in Sec. 5.1 and Sec. 5.3, respectively, while the Key Schedule is described in Sec. 5.2.

5.1 Cipher

At the start of the Cipher, the input is copied to the State array using the conventions described in Sec. 3.4. After an initial Round Key addition, the State array is transformed by implementing a round function 10, 12, or 14 times (depending on the key length), with the final round differing slightly from the first Nr - 1 rounds. The final State is then copied to the output as described in Sec. 3.4.

The round function is parameterized using a key schedule that consists of a one-dimensional array of four-byte words derived using the Key Expansion routine described in Sec. 5.2.

The Cipher is described in the pseudo code in Fig. 5. The individual transformations û SubBytes(), ShiftRows(), MixColumns(), and AddRoundKey() û process the State and are described in the following subsections. In Fig. 5, the array w[] contains the key schedule, which is described in Sec. 5.2.

As shown in Fig. 5, all Nr rounds are identical with the exception of the final round, which does not include the MixColumns() transformation.

Appendix B presents an example of the Cipher, showing values for the State array at the beginning of each round and after the application of each of the four transformations described in the following sections.

Figure 5. Pseudo Code for the Cipher.1

____________________

1 The various transformations (e.g., SubBytes(), ShiftRows(), etc.) act upon the State array that is addressed by the æstateÆ pointer. AddRoundKey() uses an additional pointer to address the Round Key.

5.1.1 SubBytes()Transformation

The SubBytes() transformation is a non-linear byte substitution that operates independently on each byte of the State using a substitution table (S-box). This S-box (Fig. 7), which is invertible, is constructed by composing two transformations:

1. Take the multiplicative inverse in the finite field GF(28), described in Sec. 4.2; the element {00} is mapped to itself.

2. Apply the following affine transformation (over GF(2) ):

b'i = bib(i+4)mod 8b(i+5)mod 8b(i+6)mod 8b(i+7)mod 8ci á á á á á á (5.1)

for 0 < i < 8, where bi is the ith bit of the byte, and ci is the ith bit of a byte c with the value {63} or {01100011}. Here and elsewhere, a prime on a variable (e.g., b' ) indicates that the variable is to be updated with the value on the right.

In matrix form, the affine transformation element of the S-box can be expressed as:

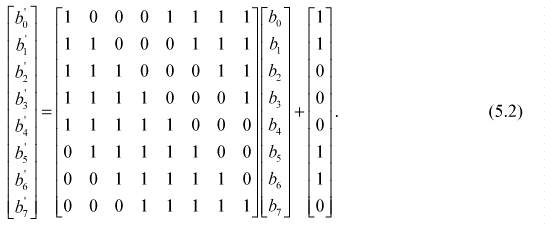
Figure 6 illustrates the effect of the SubBytes() transformation on the State.

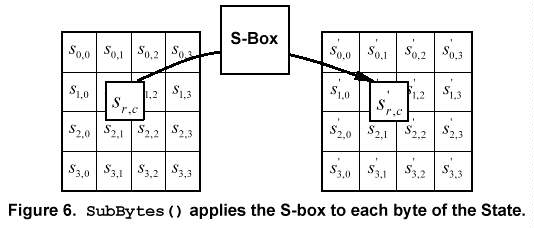
The S-box used in the SubBytes() transformation is presented in hexadecimal form in Fig. 7. For example, if s1,1 ={53}, then the substitution value would be determined by the intersection of the row with index æ5Æ and the column with index æ3Æ in Fig. 7. This would result in s'1,1 having a value of {ed}.

Figure 7. S-box: substitution values for the byte xy (in hexadecimal format).

5.1.2 ShiftRows() Transformation

In the ShiftRows() transformation, the bytes in the last three rows of the State are cyclically shifted over different numbers of bytes (offsets). The first row, r = 0, is not shifted.

Specifically, the ShiftRows() transformation proceeds as follows:

s'r,c = sr,(c + shift(r,Nb))mod Nb for 0 < r < 4 áand á0 < c Nb, á á á á á á á (5.3)

where the shift value shift(r,Nb) depends on the row number, r, as follows (recall Nb = 4):

shift(1,4) = 1; shift(2,4) = 2; shift(3,4) = 3. á á á á á á á á á á á ááá(5.4)

This has the effect of moving bytes to ôlowerö positions in the row (i.e., lower values of c in a given row), while the ôlowestö bytes wrap around into the ôtopö of the row (i.e., higher values of c in a given row).

Figure 8 illustrates the ShiftRows() transformation.

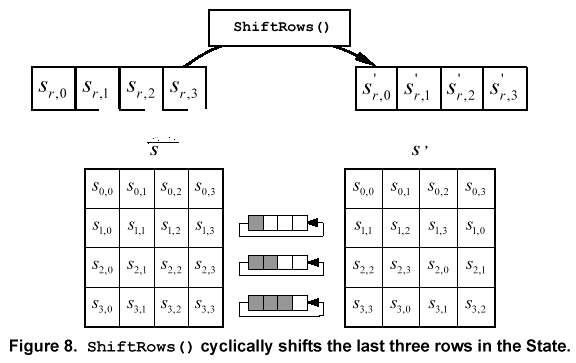
5.1.3 MixColumns() Transformation

The MixColumns() transformation operates on the State column-by-column, treating each column as a four-term polynomial as described in Sec. 4.3. The columns are considered as polynomials over GF(28) and multiplied modulo x4 + 1 with a fixed polynomial a(x), given by

a(x) = {03}x3 + {01}x2 + {01}x + {02}. á á á á á á á á á á á á (5.5)

As described in Sec. 4.3, this can be written as a matrix multiplication. Let s'(x) = a(x)s(x):

Figure 9 illustrates the MixColumns() transformation.

5.1.4 AddRoundKey() Transformation

In the AddRoundKey() transformation, a Round Key is added to the State by a simple bitwise XOR operation. Each Round Key consists of Nb words from the key schedule (described in Sec. 5.2). Those Nb words are each added into the columns of the State, such that

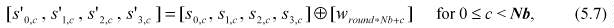
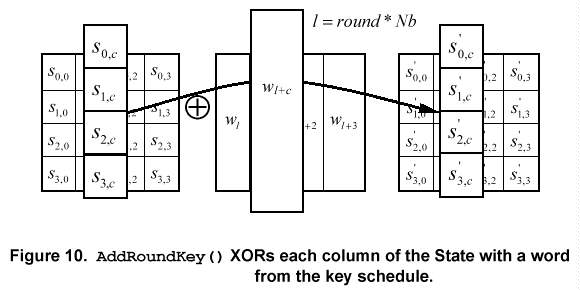
where [wi] are the key schedule words described in Sec. 5.2, and round is a value in the range 0 < round < Nr. In the Cipher, the initial Round Key addition occurs when round = 0, prior to the first application of the round function (see Fig. 5). The application of the AddRoundKey() transformation to the Nr rounds of the Cipher occurs when 1 < round < Nr.

The action of this transformation is illustrated in Fig. 10, where l = round * Nb. The byte address within words of the key schedule was described in Sec. 3.1.

5.2 Key Expansion

The AES algorithm takes the Cipher Key, K, and performs a Key Expansion routine to generate a key schedule. The Key Expansion generates a total of Nb (Nr + 1) words: the algorithm requires an initial set of Nb words, and each of the Nr rounds requires Nb words of key data. The resulting key schedule consists of a linear array of 4-byte words, denoted [wi], with i in the range 0 < i < Nb(Nr + 1).

The expansion of the input key into the key schedule proceeds according to the pseudo code in Fig. 11.

SubWord() is a function that takes a four-byte input word and applies the S-box (Sec. 5.1.1, Fig. 7) to each of the four bytes to produce an output word. The function RotWord() takes a word [a0,a1,a2,a3] as input, performs a cyclic permutation, and returns the word [a1,a2,a3,a0]. The round constant word array, Rcon[i], contains the values given by [xi-1,{00},{00},{00}], with xi-1 being powers of x (x is denoted as {02}) in the field GF(28), as discussed in Sec. 4.2 (note that i starts at 1, not 0).

From Fig. 11, it can be seen that the first Nk words of the expanded key are filled with the Cipher Key. Every following word, w[i], is equal to the XOR of the previous word, w[i-1], and the word Nk positions earlier, w[i-Nk]. For words in positions that are a multiple of Nk, a transformation is applied to w[i-1] prior to the XOR, followed by an XOR with a round constant, Rcon[i]. This transformation consists of a cyclic shift of the bytes in a word (RotWord()), followed by the application of a table lookup to all four bytes of the word (SubWord()).

It is important to note that the Key Expansion routine for 256-bit Cipher Keys (Nk = 8) is slightly different than for 128- and 192-bit Cipher Keys. If Nk = 8 and i-4 is a multiple of Nk, then SubWord() is applied to w[i-1] prior to the XOR.

Figure 11. Pseudo Code for Key Expansion.2

____________________

2 The functions SubWord() and RotWord() return a result that is a transformation of the function input, whereas the transformations in the Cipher and Inverse Cipher (e.g., ShiftRows(), SubBytes(), etc.) transform the State array that is addressed by the æstateÆ pointer.

Appendix A presents examples of the Key Expansion.

5.3 Inverse Cipher

The Cipher transformations in Sec. 5.1 can be inverted and then implemented in reverse order to produce a straightforward Inverse Cipher for the AES algorithm. The individual transformations used in the Inverse Cipher û InvShiftRows(), InvSubBytes(), InvMixColumns(), and AddRoundKey() û process the State and are described in the following subsections.

The Inverse Cipher is described in the pseudo code in Fig. 12. In Fig. 12, the array w[] contains the key schedule, which was described previously in Sec. 5.2.

Figure 12. Pseudo Code for the Inverse Cipher.3

____________________

3 The various transformations (e.g., InvSubBytes(), InvShiftRows(), etc.) act upon the State array that is addressed by the æstateÆ pointer. AddRoundKey() uses an additional pointer to address the Round Key.

5.3.1 InvShiftRows() Transformation

InvShiftRows() is the inverse of the ShiftRows() transformation. The bytes in the last three rows of the State are cyclically shifted over different numbers of bytes (offsets). The first row, r = 0, is not shifted. The bottom three rows are cyclically shifted by Nb - shift(r,Nb) bytes, where the shift value shift(r,Nb) depends on the row number, and is given in equation (5.4) (see Sec. 5.1.2).

Specifically, the InvShiftRows() transformation proceeds as follows:

s'r,c = sr,(c + shift(r,Nb))mod Nb = s'r,c á áfor 0 < r < 4 áand á0 < c Nb, á á á á á á á (5.8)

Figure 13 illustrates the InvShiftRows() transformation.

5.3.2 InvSubBytes() Transformation

InvSubBytes() is the inverse of the byte substitution transformation, in which the inverse S-box is applied to each byte of the State. This is obtained by applying the inverse of the affine transformation (5.1) followed by taking the multiplicative inverse in GF(28).

The inverse S-box used in the InvSubBytes() transformation is presented in Fig. 14:

Figure 14. Inverse S-box: substitution values for the byte xy (in
hexadecimal format).

5.3.3 InvMixColumns() Transformation

InvMixColumns() is the inverse of the MixColumns() transformation. InvMixColumns() operates on the State column-by-column, treating each column as a four-term polynomial as described in Sec. 4.3. The columns are considered as polynomials over GF(28) and multiplied modulo x4 + 1 with a fixed polynomial a-1(x), given by

5.3.4 Inverse of the AddRoundKey() Transformation

AddRoundKey(), which was described in Sec. 5.1.4, is its own inverse, since it only involves an application of the XOR operation.

5.3.5 Equivalent Inverse Cipher

In the straightforward Inverse Cipher presented in Sec. 5.3 and Fig. 12, the sequence of the transformations differs from that of the Cipher, while the form of the key schedules for encryption and decryption remains the same. However, several properties of the AES algorithm allow for an Equivalent Inverse Cipher that has the same sequence of transformations as the Cipher (with the transformations replaced by their inverses). This is accomplished with a change in the key schedule.

The two properties that allow for this Equivalent Inverse Cipher are as follows:

1. The SubBytes() and ShiftRows() transformations commute; that is, a SubBytes() transformation immediately followed by a ShiftRows() transformation is equivalent to a ShiftRows() transformation immediately followed buy a SubBytes() transformation. The same is true for their inverses, InvSubBytes() and InvShiftRows.

2. The column mixing operations - MixColumns() and InvMixColumns() - are linear with respect to the column input, which means

InvMixColumns(state XOR Round Key) =

               InvMixColumns(state) XOR InvMixColumns(Round Key).

These properties allow the order of InvSubBytes() and InvShiftRows() transformations to be reversed. The order of the AddRoundKey() and InvMixColumns() transformations can also be reversed, provided that the columns (words) of the decryption key schedule are modified using the InvMixColumns() transformation.

The equivalent inverse cipher is defined by reversing the order of the InvSubBytes() and InvShiftRows() transformations shown in Fig. 12, and by reversing the order of the AddRoundKey() and InvMixColumns() transformations used in the ôround loopö after first modifying the decryption key schedule for round = 1 to Nr-1 using the InvMixColumns() transformation. The first and last Nb words of the decryption key schedule shall not be modified in this manner.

Given these changes, the resulting Equivalent Inverse Cipher offers a more efficient structure than the Inverse Cipher described in Sec. 5.3 and Fig. 12. Pseudo code for the Equivalent Inverse Cipher appears in Fig. 15. (The word array dw[] contains the modified decryption key schedule. The modification to the Key Expansion routine is also provided in Fig. 15.)

Figure 15. Pseudo Code for the Equivalent Inverse Cipher.

6. Implementation Issues

6.1 Key Length Requirements

An implementation of the AES algorithm shall support at least one of the three key lengths specified in Sec. 5: 128, 192, or 256 bits (i.e., Nk = 4, 6, or 8, respectively). Implementations may optionally support two or three key lengths, which may promote the interoperability of algorithm implementations.

6.2 Keying Restrictions

No weak or semi-weak keys have been identified for the AES algorithm, and there is no restriction on key selection.

6.3 Parameterization of Key Length, Block Size, and Round Number

This standard explicitly defines the allowed values for the key length (Nk), block size (Nb), and number of rounds (Nr) û see Fig. 4. However, future reaffirmations of this standard could include changes or additions to the allowed values for those parameters. Therefore, implementers may choose to design their AES implementations with future flexibility in mind.

6.4 Implementation Suggestions Regarding Various Platforms

Implementation variations are possible that may, in many cases, offer performance or other advantages. Given the same input key and data (plaintext or ciphertext), any implementation that produces the same output (ciphertext or plaintext) as the algorithm specified in this standard is an acceptable implementation of the AES.

Reference [3] and other papers located at Ref. [1] include suggestions on how to efficiently implement the AES algorithm on a variety of platforms.

Appendix A - Key Expansion Examples

This appendix shows the development of the key schedule for various key sizes. Note that multi-byte values are presented using the notation described in Sec. 3. The intermediate values produced during the development of the key schedule (see Sec. 5.2) are given in the following table (all values are in hexadecimal format, with the exception of the index column (i)).

A.1 Expansion of a 128-bit Cipher Key

This section contains the key expansion of the following cipher key:

     Cipher Key = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c

for Nk = 4, which results in

        w0 = 2b7e1516  w1 = 28aed2a6  w2 = abf71588  w3 = 09cf4f3c

___________________________________________________________________________

                                                                   w[i]=

  i   temp      After     After                After XOR           temp XOR

(dec)           RotWord() SubWord() Rcon[i/Nk] with Rcon w[iûNk]   w[i-Nk]

___________________________________________________________________________

  4   09cf4f3c  cf4f3c09  8a84eb01  01000000   8b84eb01  2b7e1516  a0fafe17

  5   a0fafe17                                           28aed2a6  88542cb1

  6   88542cb1                                           abf71588  23a33939

  7   23a33939                                           09cf4f3c  2a6c7605

  8   2a6c7605  6c76052a  50386be5  02000000   52386be5  a0fafe17  f2c295f2

  9   f2c295f2                                           88542cb1  7a96b943

10   7a96b943                                           23a33939  5935807a

11   5935807a                                           2a6c7605  7359f67f

12   7359f67f  59f67f73  cb42d28f  04000000   cf42d28f  f2c295f2  3d80477d

13   3d80477d                                           7a96b943  4716fe3e

14   4716fe3e                                           5935807a  1e237e44

15   1e237e44                                           7359f67f  6d7a883b

16   6d7a883b  7a883b6d  dac4e23c  08000000   d2c4e23c  3d80477d  ef44a541

17   ef44a541                                           4716fe3e  a8525b7f

18   a8525b7f                                           1e237e44  b671253b

19   b671253b                                           6d7a883b  db0bad00

20   db0bad00  0bad00db  2b9563b9  10000000   3b9563b9  ef44a541  d4d1c6f8

21   d4d1c6f8                                           a8525b7f  7c839d87

22   7c839d87                                           b671253b  caf2b8bc

23   caf2b8bc                                           db0bad00  11f915bc

24   11f915bc  f915bc11  99596582  20000000   b9596582  d4d1c6f8  6d88a37a

25   6d88a37a                                           7c839d87  110b3efd

26   110b3efd                                           caf2b8bc  dbf98641

27   dbf98641                                           11f915bc  ca0093fd

28   ca0093fd  0093fdca  63dc5474  40000000   23dc5474  6d88a37a  4e54f70e

29   4e54f70e                                           110b3efd  5f5fc9f3

30   5f5fc9f3                                           dbf98641  84a64fb2

31   84a64fb2                                           ca0093fd  4ea6dc4f

32   4ea6dc4f  a6dc4f4e  2486842f  80000000   a486842f  4e54f70e  ead27321

33   ead27321                                           5f5fc9f3  b58dbad2

34   b58dbad2                                           84a64fb2  312bf560

35   312bf560                                           4ea6dc4f  7f8d292f

36   7f8d292f  8d292f7f  5da515d2  1b000000   46a515d2  ead27321  ac7766f3

37   ac7766f3                                           b58dbad2  19fadc21

38   19fadc21                                           312bf560  28d12941

39   28d12941                                           7f8d292f  575c006e

40   575c006e  5c006e57  4a639f5b  36000000   7c639f5b  ac7766f3  d014f9a8

41   d014f9a8                                           19fadc21  c9ee2589

42   c9ee2589                                           28d12941  e13f0cc8

43   e13f0cc8                                           575c006e  b6630ca6

___________________________________________________________________________

A.2 Expansion of a 192-bit Cipher Key

This section contains the key expansion of the following cipher key:

     Cipher Key =    8e 73 b0 f7 da 0e 64 52 c8 10 f3 2b

                     80 90 79 e5 62 f8 ea d2 52 2c 6b 7b

for Nk = 6, which results in

    w0 = 8e73b0f7  w1 = da0e6452  w2 = c810f32b  w3 = 809079e5

    w4 = 62f8ead2  w5 = 522c6b7b

___________________________________________________________________________

                                                                   w[i]=

  i   temp      After     After                After XOR           temp XOR

(dec)           RotWord() SubWord() Rcon[i/Nk] with Rcon w[iûNk]   w[i-Nk]

___________________________________________________________________________

  6   522c6b7b  2c6b7b52  717f2100  01000000   707f2100  8e73b0f7  fe0c91f7

  7   fe0c91f7                                           da0e6452  2402f5a5

  8   2402f5a5                                           c810f32b  ec12068e

  9   ec12068e                                           809079e5  6c827f6b

10   6c827f6b                                           62f8ead2  0e7a95b9

11   0e7a95b9                                           522c6b7b  5c56fec2

12   5c56fec2  56fec25c  b1bb254a  02000000   b3bb254a  fe0c91f7  4db7b4bd

13   4db7b4bd                                           2402f5a5  69b54118

14   69b54118                                           ec12068e  85a74796

15   85a74796                                           6c827f6b  e92538fd

16   e92538fd                                           0e7a95b9  e75fad44

17   e75fad44                                           5c56fec2  bb095386

18   bb095386  095386bb  01ed44ea  04000000   05ed44ea  4db7b4bd  485af057

19   485af057                                           69b54118  21efb14f

20   21efb14f                                           85a74796  a448f6d9

21   a448f6d9                                           e92538fd  4d6dce24

22   4d6dce24                                           e75fad44  aa326360

23   aa326360                                           bb095386  113b30e6

24   113b30e6  3b30e611  e2048e82  08000000   ea048e82  485af057  a25e7ed5

25   a25e7ed5                                           21efb14f  83b1cf9a

26   83b1cf9a                                           a448f6d9  27f93943

27   27f93943                                           4d6dce24  6a94f767

28   6a94f767                                           aa326360  c0a69407

29   c0a69407                                           113b30e6  d19da4e1

30   d19da4e1  9da4e1d1  5e49f83e  10000000   4e49f83e  a25e7ed5  ec1786eb

31   ec1786eb                                           83b1cf9a  6fa64971

32   6fa64971                                           27f93943  485f7032

33   485f7032                                           6a94f767  22cb8755

34   22cb8755                                           c0a69407  e26d1352

35   e26d1352                                           d19da4e1  33f0b7b3

36   33f0b7b3  f0b7b333  8ca96dc3  20000000   aca96dc3  ec1786eb  40beeb28

37   40beeb28                                           6fa64971  2f18a259

38   2f18a259                                           485f7032  6747d26b

39   6747d26b                                           22cb8755  458c553e

40   458c553e                                           e26d1352  a7e1466c

41   a7e1466c                                           33f0b7b3  9411f1df

42   9411f1df  11f1df94  82a19e22  40000000   c2a19e22  40beeb28  821f750a

43   821f750a                                           2f18a259  ad07d753

44   ad07d753                                           6747d26b  ca400538

45   ca400538                                           458c553e  8fcc5006

46   8fcc5006                                           a7e1466c  282d166a

47   282d166a                                           9411f1df  bc3ce7b5

48   bc3ce7b5  3ce7b5bc  eb94d565  80000000   6b94d565  821f750a  e98ba06f

49   e98ba06f                                           ad07d753  448c773c

50   448c773c                                           ca400538  8ecc7204

51   8ecc7204                                           8fcc5006  01002202

___________________________________________________________________________

A.3 Expansion of a 256-bit Cipher Key

This section contains the key expansion of the following cipher key:

     Cipher Key =     60 3d eb 10 15 ca 71 be 2b 73 ae f0 85 7d 77 81

                      1f 35 2c 07 3b 61 08 d7 2d 98 10 a3 09 14 df f4

for Nk = 8, which results in

    w0 = 603deb10  w1 = 15ca71be  w2 = 2b73aef0  w3 = 857d7781

    w4 = 1f352c07  w5 = 3b6108d7  w6 = 2d9810a3  w7 = 0914dff4

___________________________________________________________________________

                                                                   w[i]=

  i   temp      After     After                After XOR           temp XOR

(dec)           RotWord() SubWord() Rcon[i/Nk] with Rcon w[iûNk]   w[i-Nk]

___________________________________________________________________________

  8   0914dff4  14dff409  fa9ebf01  01000000   fb9ebf01  603deb10  9ba35411

  9   9ba35411                                           15ca71be  8e6925af

10   8e6925af                                           2b73aef0  a51a8b5f

11   a51a8b5f                                           857d7781  2067fcde

12   2067fcde            b785b01d                       1f352c07  a8b09c1a

13   a8b09c1a                                           3b6108d7  93d194cd

14   93d194cd                                           2d9810a3  be49846e

15   be49846e                                           0914dff4  b75d5b9a

16   b75d5b9a  5d5b9ab7  4c39b8a9  02000000   4e39b8a9  9ba35411  d59aecb8

17   d59aecb8                                           8e6925af  5bf3c917

18   5bf3c917                                           a51a8b5f  fee94248

19   fee94248                                           2067fcde  de8ebe96

20   de8ebe96            1d19ae90                       a8b09c1a  b5a9328a

21   b5a9328a                                           93d194cd  2678a647

22   2678a647                                           be49846e  98312229

23   98312229                                           b75d5b9a  2f6c79b3

24   2f6c79b3  6c79b32f  50b66d15  04000000   54b66d15  d59aecb8  812c81ad

25   812c81ad                                           5bf3c917  dadf48ba

26   dadf48ba                                           fee94248  24360af2

27   24360af2                                           de8ebe96  fab8b464

28   fab8b464            2d6c8d43                       b5a9328a  98c5bfc9

29   98c5bfc9                                           2678a647  bebd198e

30   bebd198e                                           98312229  268c3ba7

31   268c3ba7                                           2f6c79b3  09e04214

32   09e04214  e0421409  e12cfa01  08000000   e92cfa01  812c81ad  68007bac

33   68007bac                                           dadf48ba  b2df3316

34   b2df3316                                           24360af2  96e939e4

35   96e939e4                                           fab8b464  6c518d80

36   6c518d80            50d15dcd                       98c5bfc9  c814e204

37   c814e204                                           bebd198e  76a9fb8a

38   76a9fb8a                                           268c3ba7  5025c02d

39   5025c02d                                           09e04214  59c58239

40   59c58239  c5823959  a61312cb  10000000   b61312cb  68007bac  de136967

41   de136967                                           b2df3316  6ccc5a71

42   6ccc5a71                                           96e939e4  fa256395

43   fa256395                                           6c518d80  9674ee15

44   9674ee15            90922859                       c814e204  5886ca5d

45   5886ca5d                                           76a9fb8a  2e2f31d7

46   2e2f31d7                                           5025c02d  7e0af1fa

47   7e0af1fa                                           59c58239  27cf73c3

48   27cf73c3  cf73c327  8a8f2ecc  20000000   aa8f2ecc  de136967  749c47ab

49   749c47ab                                           6ccc5a71  18501dda

50   18501dda                                           fa256395  e2757e4f

51   e2757e4f                                           9674ee15  7401905a

52   7401905a            927c60be                       5886ca5d  cafaaae3

53   cafaaae3                                           2e2f31d7  e4d59b34

54   e4d59b34                                           7e0af1fa  9adf6ace

55   9adf6ace                                           27cf73c3  bd10190d

56   bd10190d  10190dbd  cad4d77a  40000000   8ad4d77a  749c47ab  fe4890d1

57   fe4890d1                                           18501dda  e6188d0b

58   e6188d0b                                           e2757e4f  046df344

59   046df344                                           7401905a  706c631e

___________________________________________________________________________

Appendix B û Cipher Example

The following diagram shows the values in the State array as the Cipher progresses for a block length and a Cipher Key length of 16 bytes each (i.e., Nb = 4 and Nk = 4).

     Input = 32 43 f6 a8 88 5a 30 8d 31 31 98 a2 e0 37 07 34

     Cipher Key = 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 09 cf 4f 3c

The Round Key values are taken from the Key Expansion example in Appendix A.

Round   Start of      After          After         After        Round Key

Number    Round       SubBytes      ShiftRows     MixColumns       Value

       32 88 31 e0                                              2b 28 ab 09

input  43 5a 31 37                                           7e ae f7 cf  =

       f6 30 98 07                                              15 d2 15 4f

       a8 8d a2 34                                              16 a6 88 3c

       19 a0 9a e9   d4 e0 b8 1e   d4 e0 b8 1e   04 e0 48 28    a0 88 23 2a

  1    3d f4 c6 f8   27 bf b4 41   bf b4 41 27   66 cb f8 06 fa 54 a3 6c  =

       e3 e2 8d 48   11 98 5d 52   5d 52 11 98   81 19 d3 26    fe 2c 39 76

       be 2b 2a 08   ae f1 e5 30   30 ae f1 e5   e5 9a 7a 4c    17 b1 39 05

       a4 68 6b 02   49 45 7f 77   49 45 7f 77   58 1b db 1b     f2 7a 59 73

  2    9c 9f 5b 6a   de db 39 02   db 39 02 de   4d 4b e7 6b c2 96 35 59  =

       7f 35 ea 50   d2 96 87 53   87 53 d2 96   ca 5a ca b0    95 b9 80 f6

       f2 2b 43 49   89 f1 1a 3b   3b 89 f1 1a   f1 ac a8 e5    f2 43 7a 7f

       aa 61 82 68   ac ef 13 45   ac ef 13 45   75 20 53 bb    3d 47 1e 6d

  3    8f dd d2 32   73 c1 b5 23   c1 b5 23 73   ec 0b c0 25 80 16 23 7a  =

       5f e3 4a 46   cf 11 d6 5a   d6 5a cf 11   09 63 cf d0    47 fe 7e 88

       03 ef d2 9a   7b df b5 b8   b8 7b df b5   93 33 7c dc    7d 3e 44 3b

       48 67 4d d6   52 85 e3 f6   52 85 e3 f6   0f 60 6f 5e    ef a8 b6 db

  4    6c 1d e3 5f   50 a4 11 cf   a4 11 cf 50   d6 31 c0 b3 44 52 71 0b  =

       4e 9d b1 58   2f 5e c8 6a   c8 6a 2f 5e   da 38 10 13    a5 5b 25 ad

       ee 0d 38 e7   28 d7 07 94   94 28 d7 07   a9 bf 6b 01    41 7f 3b 00

       e0 c8 d9 85   e1 e8 35 97   e1 e8 35 97   25 bd b6 4c    d4 7c ca 11

  5    92 63 b1 b8   4f fb c8 6c   fb c8 6c 4f   d1 11 3a 4c d1 83 f2 f9  =

       7f 63 35 be   d2 fb 96 ae   96 ae d2 fb   a9 d1 33 c0    c6 9d b8 15

       e8 c0 50 01   9b ba 53 7c   7c 9b ba 53   ad 68 8e b0    f8 87 bc bc

       f1 c1 7c 5d   a1 78 10 4c   a1 78 10 4c   4b 2c 33 37    6d 11 db ca

  6    00 92 c8 b5   63 4f e8 d5   4f e8 d5 63   86 4a 9d d2 88 0b f9 00  =

       6f 4c 8b d5   a8 29 3d 03   3d 03 a8 29   8d 89 f4 18    a3 3e 86 93

       55 ef 32 0c   fc df 23 fe   fe fc df 23   6d 80 e8 d8    7a fd 41 fd

       26 3d e8 fd   f7 27 9b 54   f7 27 9b 54   14 46 27 34    4e 5f 84 4e

  7    0e 41 64 d2   ab 83 43 b5   83 43 b5 ab   15 16 46 2a 54 5f a6 a6  =

       2e b7 72 8b   31 a9 40 3d   40 3d 31 a9   b5 15 56 d8    f7 c9 4f dc

       17 7d a9 25   f0 ff d3 3f   3f f0 ff d3   bf ec d7 43    0e f3 b2 4f

       5a 19 a3 7a   be d4 0a da   be d4 0a da   00 b1 54 fa    ea b5 31 7f

  8    41 49 e0 8c   83 3b e1 64   3b e1 64 83   51 c8 76 1b d2 8d 2b 8d  =

       42 dc 19 04   2c 86 d4 f2   d4 f2 2c 86   2f 89 6d 99    73 ba f5 29

       b1 1f 65 0c   c8 c0 4d fe   fe c8 c0 4d   d1 ff cd ea    21 d2 60 2f

       ea 04 65 85   87 f2 4d 97   87 f2 4d 97   47 40 a3 4c    ac 19 28 57

  9    83 45 5d 96   ec 6e 4c 90   6e 4c 90 ec   37 d4 70 9f 77 fa d1 5c  =

       5c 33 98 b0   4a c3 46 e7   46 e7 4a c3   94 e4 3a 42    66 dc 29 00

       f0 2d ad c5   8c d8 95 a6   a6 8c d8 95   ed a5 a6 bc    f3 21 41 6e

       eb 59 8b 1b   e9 cb 3d af   e9 cb 3d af                  d0 c9 e1 b6

  10   40 2e a1 c3   09 31 32 2e   31 32 2e 09               14 ee 3f 63  =

       f2 38 13 42   89 07 7d 2c   7d 2c 89 07                  f9 25 0c 0c

       1e 84 e7 d2   72 5f 94 b5   b5 72 5f 94                  a8 89 c8 a6

       39 02 dc 19

output 25 dc 11 6a

       84 09 85 0b

       1d fb 97 32

Appendix C û Example Vectors

This appendix contains example vectors, including intermediate values û for all three AES key lengths (Nk = 4, 6, and 8), for the Cipher, Inverse Cipher, and Equivalent Inverse Cipher that are described in Sec. 5.1, 5.3, and 5.3.5, respectively. Additional examples may be found at [1] and [5].

All vectors are in hexadecimal notation, with each pair of characters giving a byte value in which the left character of each pair provides the bit pattern for the 4 bit group containing the higher numbered bits using the notation explained in Sec. 3.2, while the right character provides the bit pattern for the lower-numbered bits. The array index for all bytes (groups of two hexadecimal digits) within these test vectors starts at zero and increases from left to right.

Legend for CIPHER (ENCRYPT) (round number r = 0 to 10, 12 or 14):

   input: cipher input

   start: state at start of round[r]

   s_box: state after SubBytes()

   s_row: state after ShiftRows()

   m_col: state after MixColumns()

   k_sch: key schedule value for round[r]

   output: cipher output

Legend for INVERSE CIPHER (DECRYPT) (round number r = 0 to 10, 12 or 14):

   iinput: inverse cipher input

   istart: state at start of round[r]

   is_box: state after InvSubBytes()

   is_row: state after InvShiftRows()

   ik_sch: key schedule value for round[r]

   ik_add: state after AddRoundKey()

   ioutput: inverse cipher output

Legend for EQUIVALENT INVERSE CIPHER (DECRYPT) (round number r = 0 to 10, 12

   or 14):

   iinput: inverse cipher input

   istart: state at start of round[r]

   is_box: state after InvSubBytes()

   is_row: state after InvShiftRows()

   im_col: state after InvMixColumns()

   ik_sch: key schedule value for round[r]

   ioutput: inverse cipher output

C.1 AES-128 (Nk=4, Nr=10)

PLAINTEXT:        00112233445566778899aabbccddeeff

KEY:              000102030405060708090a0b0c0d0e0f

CIPHER (ENCRYPT):

round[ 0].input   00112233445566778899aabbccddeeff

round[ 0].k_sch   000102030405060708090a0b0c0d0e0f

round[ 1].start   00102030405060708090a0b0c0d0e0f0

round[ 1].s_box   63cab7040953d051cd60e0e7ba70e18c

round[ 1].s_row   6353e08c0960e104cd70b751bacad0e7

round[ 1].m_col   5f72641557f5bc92f7be3b291db9f91a

round[ 1].k_sch   d6aa74fdd2af72fadaa678f1d6ab76fe

round[ 2].start   89d810e8855ace682d1843d8cb128fe4

round[ 2].s_box   a761ca9b97be8b45d8ad1a611fc97369

round[ 2].s_row   a7be1a6997ad739bd8c9ca451f618b61

round[ 2].m_col   ff87968431d86a51645151fa773ad009

round[ 2].k_sch   b692cf0b643dbdf1be9bc5006830b3fe

round[ 3].start   4915598f55e5d7a0daca94fa1f0a63f7

round[ 3].s_box   3b59cb73fcd90ee05774222dc067fb68

round[ 3].s_row   3bd92268fc74fb735767cbe0c0590e2d

round[ 3].m_col   4c9c1e66f771f0762c3f868e534df256

round[ 3].k_sch   b6ff744ed2c2c9bf6c590cbf0469bf41

round[ 4].start   fa636a2825b339c940668a3157244d17

round[ 4].s_box   2dfb02343f6d12dd09337ec75b36e3f0

round[ 4].s_row   2d6d7ef03f33e334093602dd5bfb12c7

round[ 4].m_col   6385b79ffc538df997be478e7547d691

round[ 4].k_sch   47f7f7bc95353e03f96c32bcfd058dfd

round[ 5].start   247240236966b3fa6ed2753288425b6c

round[ 5].s_box   36400926f9336d2d9fb59d23c42c3950

round[ 5].s_row   36339d50f9b539269f2c092dc4406d23

round[ 5].m_col   f4bcd45432e554d075f1d6c51dd03b3c

round[ 5].k_sch   3caaa3e8a99f9deb50f3af57adf622aa

round[ 6].start   c81677bc9b7ac93b25027992b0261996

round[ 6].s_box   e847f56514dadde23f77b64fe7f7d490

round[ 6].s_row   e8dab6901477d4653ff7f5e2e747dd4f

round[ 6].m_col   9816ee7400f87f556b2c049c8e5ad036

round[ 6].k_sch   5e390f7df7a69296a7553dc10aa31f6b

round[ 7].start   c62fe109f75eedc3cc79395d84f9cf5d

round[ 7].s_box   b415f8016858552e4bb6124c5f998a4c

round[ 7].s_row   b458124c68b68a014b99f82e5f15554c

round[ 7].m_col   c57e1c159a9bd286f05f4be098c63439

round[ 7].k_sch   14f9701ae35fe28c440adf4d4ea9c026

round[ 8].start   d1876c0f79c4300ab45594add66ff41f

round[ 8].s_box   3e175076b61c04678dfc2295f6a8bfc0

round[ 8].s_row   3e1c22c0b6fcbf768da85067f6170495

round[ 8].m_col   baa03de7a1f9b56ed5512cba5f414d23

round[ 8].k_sch   47438735a41c65b9e016baf4aebf7ad2

round[ 9].start   fde3bad205e5d0d73547964ef1fe37f1

round[ 9].s_box   5411f4b56bd9700e96a0902fa1bb9aa1

round[ 9].s_row   54d990a16ba09ab596bbf40ea111702f

round[ 9].m_col   e9f74eec023020f61bf2ccf2353c21c7

round[ 9].k_sch   549932d1f08557681093ed9cbe2c974e

round[10].start   bd6e7c3df2b5779e0b61216e8b10b689

round[10].s_box   7a9f102789d5f50b2beffd9f3dca4ea7

round[10].s_row   7ad5fda789ef4e272bca100b3d9ff59f

round[10].k_sch   13111d7fe3944a17f307a78b4d2b30c5

round[10].output  69c4e0d86a7b0430d8cdb78070b4c55a

INVERSE CIPHER (DECRYPT):

round[ 0].iinput   69c4e0d86a7b0430d8cdb78070b4c55a

round[ 0].ik_sch   13111d7fe3944a17f307a78b4d2b30c5

round[ 1].istart   7ad5fda789ef4e272bca100b3d9ff59f

round[ 1].is_row   7a9f102789d5f50b2beffd9f3dca4ea7

round[ 1].is_box   bd6e7c3df2b5779e0b61216e8b10b689

round[ 1].ik_sch   549932d1f08557681093ed9cbe2c974e

round[ 1].ik_add   e9f74eec023020f61bf2ccf2353c21c7

round[ 2].istart   54d990a16ba09ab596bbf40ea111702f

round[ 2].is_row   5411f4b56bd9700e96a0902fa1bb9aa1

round[ 2].is_box   fde3bad205e5d0d73547964ef1fe37f1

round[ 2].ik_sch   47438735a41c65b9e016baf4aebf7ad2

round[ 2].ik_add   baa03de7a1f9b56ed5512cba5f414d23

round[ 3].istart   3e1c22c0b6fcbf768da85067f6170495

round[ 3].is_row   3e175076b61c04678dfc2295f6a8bfc0

round[ 3].is_box   d1876c0f79c4300ab45594add66ff41f

round[ 3].ik_sch   14f9701ae35fe28c440adf4d4ea9c026

round[ 3].ik_add   c57e1c159a9bd286f05f4be098c63439

round[ 4].istart   b458124c68b68a014b99f82e5f15554c

round[ 4].is_row   b415f8016858552e4bb6124c5f998a4c

round[ 4].is_box   c62fe109f75eedc3cc79395d84f9cf5d

round[ 4].ik_sch   5e390f7df7a69296a7553dc10aa31f6b

round[ 4].ik_add   9816ee7400f87f556b2c049c8e5ad036

round[ 5].istart   e8dab6901477d4653ff7f5e2e747dd4f

round[ 5].is_row   e847f56514dadde23f77b64fe7f7d490

round[ 5].is_box   c81677bc9b7ac93b25027992b0261996

round[ 5].ik_sch   3caaa3e8a99f9deb50f3af57adf622aa

round[ 5].ik_add   f4bcd45432e554d075f1d6c51dd03b3c

round[ 6].istart   36339d50f9b539269f2c092dc4406d23

round[ 6].is_row   36400926f9336d2d9fb59d23c42c3950

round[ 6].is_box   247240236966b3fa6ed2753288425b6c

round[ 6].ik_sch   47f7f7bc95353e03f96c32bcfd058dfd

round[ 6].ik_add   6385b79ffc538df997be478e7547d691

round[ 7].istart   2d6d7ef03f33e334093602dd5bfb12c7

round[ 7].is_row   2dfb02343f6d12dd09337ec75b36e3f0

round[ 7].is_box   fa636a2825b339c940668a3157244d17

round[ 7].ik_sch   b6ff744ed2c2c9bf6c590cbf0469bf41

round[ 7].ik_add   4c9c1e66f771f0762c3f868e534df256

round[ 8].istart   3bd92268fc74fb735767cbe0c0590e2d

round[ 8].is_row   3b59cb73fcd90ee05774222dc067fb68

round[ 8].is_box   4915598f55e5d7a0daca94fa1f0a63f7

round[ 8].ik_sch   b692cf0b643dbdf1be9bc5006830b3fe

round[ 8].ik_add   ff87968431d86a51645151fa773ad009

round[ 9].istart   a7be1a6997ad739bd8c9ca451f618b61

round[ 9].is_row   a761ca9b97be8b45d8ad1a611fc97369

round[ 9].is_box   89d810e8855ace682d1843d8cb128fe4

round[ 9].ik_sch   d6aa74fdd2af72fadaa678f1d6ab76fe

round[ 9].ik_add   5f72641557f5bc92f7be3b291db9f91a

round[10].istart   6353e08c0960e104cd70b751bacad0e7

round[10].is_row   63cab7040953d051cd60e0e7ba70e18c

round[10].is_box   00102030405060708090a0b0c0d0e0f0

round[10].ik_sch   000102030405060708090a0b0c0d0e0f

round[10].ioutput  00112233445566778899aabbccddeeff

EQUIVALENT INVERSE CIPHER (DECRYPT):

round[ 0].iinput   69c4e0d86a7b0430d8cdb78070b4c55a

round[ 0].ik_sch   13111d7fe3944a17f307a78b4d2b30c5

round[ 1].istart   7ad5fda789ef4e272bca100b3d9ff59f

round[ 1].is_box   bdb52189f261b63d0b107c9e8b6e776e

round[ 1].is_row   bd6e7c3df2b5779e0b61216e8b10b689

round[ 1].im_col   4773b91ff72f354361cb018ea1e6cf2c

round[ 1].ik_sch   13aa29be9c8faff6f770f58000f7bf03

round[ 2].istart   54d990a16ba09ab596bbf40ea111702f

round[ 2].is_box   fde596f1054737d235febad7f1e3d04e

round[ 2].is_row   fde3bad205e5d0d73547964ef1fe37f1

round[ 2].im_col   2d7e86a339d9393ee6570a1101904e16

round[ 2].ik_sch   1362a4638f2586486bff5a76f7874a83

round[ 3].istart   3e1c22c0b6fcbf768da85067f6170495

round[ 3].is_box   d1c4941f7955f40fb46f6c0ad68730ad

round[ 3].is_row   d1876c0f79c4300ab45594add66ff41f

round[ 3].im_col   39daee38f4f1a82aaf432410c36d45b9

round[ 3].ik_sch   8d82fc749c47222be4dadc3e9c7810f5

round[ 4].istart   b458124c68b68a014b99f82e5f15554c

round[ 4].is_box   c65e395df779cf09ccf9e1c3842fed5d

round[ 4].is_row   c62fe109f75eedc3cc79395d84f9cf5d

round[ 4].im_col   9a39bf1d05b20a3a476a0bf79fe51184

round[ 4].ik_sch   72e3098d11c5de5f789dfe1578a2cccb

round[ 5].istart   e8dab6901477d4653ff7f5e2e747dd4f

round[ 5].is_box   c87a79969b0219bc2526773bb016c992

round[ 5].is_row   c81677bc9b7ac93b25027992b0261996

round[ 5].im_col   18f78d779a93eef4f6742967c47f5ffd

round[ 5].ik_sch   2ec410276326d7d26958204a003f32de

round[ 6].istart   36339d50f9b539269f2c092dc4406d23

round[ 6].is_box   2466756c69d25b236e4240fa8872b332

round[ 6].is_row   247240236966b3fa6ed2753288425b6c

round[ 6].im_col   85cf8bf472d124c10348f545329c0053

round[ 6].ik_sch   a8a2f5044de2c7f50a7ef79869671294

round[ 7].istart   2d6d7ef03f33e334093602dd5bfb12c7

round[ 7].is_box   fab38a1725664d2840246ac957633931

round[ 7].is_row   fa636a2825b339c940668a3157244d17

round[ 7].im_col   fc1fc1f91934c98210fbfb8da340eb21

round[ 7].ik_sch   c7c6e391e54032f1479c306d6319e50c

round[ 8].istart   3bd92268fc74fb735767cbe0c0590e2d

round[ 8].is_box   49e594f755ca638fda0a59a01f15d7fa

round[ 8].is_row   4915598f55e5d7a0daca94fa1f0a63f7

round[ 8].im_col   076518f0b52ba2fb7a15c8d93be45e00

round[ 8].ik_sch   a0db02992286d160a2dc029c2485d561

round[ 9].istart   a7be1a6997ad739bd8c9ca451f618b61

round[ 9].is_box   895a43e485188fe82d121068cbd8ced8

round[ 9].is_row   89d810e8855ace682d1843d8cb128fe4

round[ 9].im_col   ef053f7c8b3d32fd4d2a64ad3c93071a

round[ 9].ik_sch   8c56dff0825dd3f9805ad3fc8659d7fd

round[10].istart   6353e08c0960e104cd70b751bacad0e7

round[10].is_box   0050a0f04090e03080d02070c01060b0

round[10].is_row   00102030405060708090a0b0c0d0e0f0

round[10].ik_sch   000102030405060708090a0b0c0d0e0f

round[10].ioutput  00112233445566778899aabbccddeeff

C.2 AES-192 (Nk=6, Nr=12)

PLAINTEXT:        00112233445566778899aabbccddeeff

KEY:              000102030405060708090a0b0c0d0e0f1011121314151617

CIPHER (ENCRYPT):

round[ 0].input   00112233445566778899aabbccddeeff

round[ 0].k_sch   000102030405060708090a0b0c0d0e0f

round[ 1].start   00102030405060708090a0b0c0d0e0f0

round[ 1].s_box   63cab7040953d051cd60e0e7ba70e18c

round[ 1].s_row   6353e08c0960e104cd70b751bacad0e7

round[ 1].m_col   5f72641557f5bc92f7be3b291db9f91a

round[ 1].k_sch   10111213141516175846f2f95c43f4fe

round[ 2].start   4f63760643e0aa85aff8c9d041fa0de4

round[ 2].s_box   84fb386f1ae1ac977941dd70832dd769

round[ 2].s_row   84e1dd691a41d76f792d389783fbac70

round[ 2].m_col   9f487f794f955f662afc86abd7f1ab29

round[ 2].k_sch   544afef55847f0fa4856e2e95c43f4fe

round[ 3].start   cb02818c17d2af9c62aa64428bb25fd7

round[ 3].s_box   1f770c64f0b579deaaac432c3d37cf0e

round[ 3].s_row   1fb5430ef0accf64aa370cde3d77792c

round[ 3].m_col   b7a53ecbbf9d75a0c40efc79b674cc11

round[ 3].k_sch   40f949b31cbabd4d48f043b810b7b342

round[ 4].start   f75c7778a327c8ed8cfebfc1a6c37f53

round[ 4].s_box   684af5bc0acce85564bb0878242ed2ed

round[ 4].s_row   68cc08ed0abbd2bc642ef555244ae878

round[ 4].m_col   7a1e98bdacb6d1141a6944dd06eb2d3e

round[ 4].k_sch   58e151ab04a2a5557effb5416245080c

round[ 5].start   22ffc916a81474416496f19c64ae2532

round[ 5].s_box   9316dd47c2fa92834390a1de43e43f23

round[ 5].s_row   93faa123c2903f4743e4dd83431692de

round[ 5].m_col   aaa755b34cffe57cef6f98e1f01c13e6

round[ 5].k_sch   2ab54bb43a02f8f662e3a95d66410c08

round[ 6].start   80121e0776fd1d8a8d8c31bc965d1fee

round[ 6].s_box   cdc972c53854a47e5d64c765904cc028

round[ 6].s_row   cd54c7283864c0c55d4c727e90c9a465

round[ 6].m_col   921f748fd96e937d622d7725ba8ba50c

round[ 6].k_sch   f501857297448d7ebdf1c6ca87f33e3c

round[ 7].start   671ef1fd4e2a1e03dfdcb1ef3d789b30

round[ 7].s_box   8572a1542fe5727b9e86c8df27bc1404

round[ 7].s_row   85e5c8042f8614549ebca17b277272df

round[ 7].m_col   e913e7b18f507d4b227ef652758acbcc

round[ 7].k_sch   e510976183519b6934157c9ea351f1e0

round[ 8].start   0c0370d00c01e622166b8accd6db3a2c

round[ 8].s_box   fe7b5170fe7c8e93477f7e4bf6b98071

round[ 8].s_row   fe7c7e71fe7f807047b95193f67b8e4b

round[ 8].m_col   6cf5edf996eb0a069c4ef21cbfc25762

round[ 8].k_sch   1ea0372a995309167c439e77ff12051e

round[ 9].start   7255dad30fb80310e00d6c6b40d0527c

round[ 9].s_box   40fc5766766c7bcae1d7507f09700010

round[ 9].s_row   406c501076d70066e17057ca09fc7b7f

round[ 9].m_col   7478bcdce8a50b81d4327a9009188262

round[ 9].k_sch   dd7e0e887e2fff68608fc842f9dcc154

round[10].start   a906b254968af4e9b4bdb2d2f0c44336

round[10].s_box   d36f3720907ebf1e8d7a37b58c1c1a05

round[10].s_row   d37e3705907a1a208d1c371e8c6fbfb5

round[10].m_col   0d73cc2d8f6abe8b0cf2dd9bb83d422e

round[10].k_sch   859f5f237a8d5a3dc0c02952beefd63a

round[11].start   88ec930ef5e7e4b6cc32f4c906d29414

round[11].s_box   c4cedcabe694694e4b23bfdd6fb522fa

round[11].s_row   c494bffae62322ab4bb5dc4e6fce69dd

round[11].m_col   71d720933b6d677dc00b8f28238e0fb7

round[11].k_sch   de601e7827bcdf2ca223800fd8aeda32

round[12].start   afb73eeb1cd1b85162280f27fb20d585

round[12].s_box   79a9b2e99c3e6cd1aa3476cc0fb70397

round[12].s_row   793e76979c3403e9aab7b2d10fa96ccc

round[12].k_sch   a4970a331a78dc09c418c271e3a41d5d

round[12].output  dda97ca4864cdfe06eaf70a0ec0d7191

INVERSE CIPHER (DECRYPT):

round[ 0].iinput   dda97ca4864cdfe06eaf70a0ec0d7191

round[ 0].ik_sch   a4970a331a78dc09c418c271e3a41d5d

round[ 1].istart   793e76979c3403e9aab7b2d10fa96ccc

round[ 1].is_row   79a9b2e99c3e6cd1aa3476cc0fb70397

round[ 1].is_box   afb73eeb1cd1b85162280f27fb20d585

round[ 1].ik_sch   de601e7827bcdf2ca223800fd8aeda32

round[ 1].ik_add   71d720933b6d677dc00b8f28238e0fb7

round[ 2].istart   c494bffae62322ab4bb5dc4e6fce69dd

round[ 2].is_row   c4cedcabe694694e4b23bfdd6fb522fa

round[ 2].is_box   88ec930ef5e7e4b6cc32f4c906d29414

round[ 2].ik_sch   859f5f237a8d5a3dc0c02952beefd63a

round[ 2].ik_add   0d73cc2d8f6abe8b0cf2dd9bb83d422e

round[ 3].istart   d37e3705907a1a208d1c371e8c6fbfb5

round[ 3].is_row   d36f3720907ebf1e8d7a37b58c1c1a05

round[ 3].is_box   a906b254968af4e9b4bdb2d2f0c44336

round[ 3].ik_sch   dd7e0e887e2fff68608fc842f9dcc154

round[ 3].ik_add   7478bcdce8a50b81d4327a9009188262

round[ 4].istart   406c501076d70066e17057ca09fc7b7f

round[ 4].is_row   40fc5766766c7bcae1d7507f09700010

round[ 4].is_box   7255dad30fb80310e00d6c6b40d0527c

round[ 4].ik_sch   1ea0372a995309167c439e77ff12051e

round[ 4].ik_add   6cf5edf996eb0a069c4ef21cbfc25762

round[ 5].istart   fe7c7e71fe7f807047b95193f67b8e4b

round[ 5].is_row   fe7b5170fe7c8e93477f7e4bf6b98071

round[ 5].is_box   0c0370d00c01e622166b8accd6db3a2c

round[ 5].ik_sch   e510976183519b6934157c9ea351f1e0

round[ 5].ik_add   e913e7b18f507d4b227ef652758acbcc

round[ 6].istart   85e5c8042f8614549ebca17b277272df

round[ 6].is_row   8572a1542fe5727b9e86c8df27bc1404

round[ 6].is_box   671ef1fd4e2a1e03dfdcb1ef3d789b30

round[ 6].ik_sch   f501857297448d7ebdf1c6ca87f33e3c

round[ 6].ik_add   921f748fd96e937d622d7725ba8ba50c

round[ 7].istart   cd54c7283864c0c55d4c727e90c9a465

round[ 7].is_row   cdc972c53854a47e5d64c765904cc028

round[ 7].is_box   80121e0776fd1d8a8d8c31bc965d1fee

round[ 7].ik_sch   2ab54bb43a02f8f662e3a95d66410c08

round[ 7].ik_add   aaa755b34cffe57cef6f98e1f01c13e6

round[ 8].istart   93faa123c2903f4743e4dd83431692de

round[ 8].is_row   9316dd47c2fa92834390a1de43e43f23

round[ 8].is_box   22ffc916a81474416496f19c64ae2532

round[ 8].ik_sch   58e151ab04a2a5557effb5416245080c

round[ 8].ik_add   7a1e98bdacb6d1141a6944dd06eb2d3e

round[ 9].istart   68cc08ed0abbd2bc642ef555244ae878

round[ 9].is_row   684af5bc0acce85564bb0878242ed2ed

round[ 9].is_box   f75c7778a327c8ed8cfebfc1a6c37f53

round[ 9].ik_sch   40f949b31cbabd4d48f043b810b7b342

round[ 9].ik_add   b7a53ecbbf9d75a0c40efc79b674cc11

round[10].istart   1fb5430ef0accf64aa370cde3d77792c

round[10].is_row   1f770c64f0b579deaaac432c3d37cf0e

round[10].is_box   cb02818c17d2af9c62aa64428bb25fd7

round[10].ik_sch   544afef55847f0fa4856e2e95c43f4fe

round[10].ik_add   9f487f794f955f662afc86abd7f1ab29

round[11].istart   84e1dd691a41d76f792d389783fbac70

round[11].is_row   84fb386f1ae1ac977941dd70832dd769

round[11].is_box   4f63760643e0aa85aff8c9d041fa0de4

round[11].ik_sch   10111213141516175846f2f95c43f4fe

round[11].ik_add   5f72641557f5bc92f7be3b291db9f91a

round[12].istart   6353e08c0960e104cd70b751bacad0e7

round[12].is_row   63cab7040953d051cd60e0e7ba70e18c

round[12].is_box   00102030405060708090a0b0c0d0e0f0

round[12].ik_sch   000102030405060708090a0b0c0d0e0f

round[12].ioutput  00112233445566778899aabbccddeeff

EQUIVALENT INVERSE CIPHER (DECRYPT):

round[ 0].iinput   dda97ca4864cdfe06eaf70a0ec0d7191

round[ 0].ik_sch   a4970a331a78dc09c418c271e3a41d5d

round[ 1].istart   793e76979c3403e9aab7b2d10fa96ccc

round[ 1].is_box   afd10f851c28d5eb62203e51fbb7b827

round[ 1].is_row   afb73eeb1cd1b85162280f27fb20d585

round[ 1].im_col   122a02f7242ac8e20605afce51cc7264

round[ 1].ik_sch   d6bebd0dc209ea494db073803e021bb9

round[ 2].istart   c494bffae62322ab4bb5dc4e6fce69dd

round[ 2].is_box   88e7f414f532940eccd293b606ece4c9

round[ 2].is_row   88ec930ef5e7e4b6cc32f4c906d29414

round[ 2].im_col   5cc7aecce3c872194ae5ef8309a933c7

round[ 2].ik_sch   8fb999c973b26839c7f9d89d85c68c72

round[ 3].istart   d37e3705907a1a208d1c371e8c6fbfb5

round[ 3].is_box   a98ab23696bd4354b4c4b2e9f006f4d2

round[ 3].is_row   a906b254968af4e9b4bdb2d2f0c44336

round[ 3].im_col   b7113ed134e85489b20866b51d4b2c3b

round[ 3].ik_sch   f77d6ec1423f54ef5378317f14b75744

round[ 4].istart   406c501076d70066e17057ca09fc7b7f

round[ 4].is_box   72b86c7c0f0d52d3e0d0da104055036b

round[ 4].is_row   7255dad30fb80310e00d6c6b40d0527c

round[ 4].im_col   ef3b1be1b9b0e64bdcb79f1e0a707fbb

round[ 4].ik_sch   1147659047cf663b9b0ece8dfc0bf1f0

round[ 5].istart   fe7c7e71fe7f807047b95193f67b8e4b

round[ 5].is_box   0c018a2c0c6b3ad016db7022d603e6cc

round[ 5].is_row   0c0370d00c01e622166b8accd6db3a2c

round[ 5].im_col   592460b248832b2952e0b831923048f1

round[ 5].ik_sch   dcc1a8b667053f7dcc5c194ab5423a2e

round[ 6].istart   85e5c8042f8614549ebca17b277272df

round[ 6].is_box   672ab1304edc9bfddf78f1033d1e1eef

round[ 6].is_row   671ef1fd4e2a1e03dfdcb1ef3d789b30

round[ 6].im_col   0b8a7783417ae3a1f9492dc0c641a7ce

round[ 6].ik_sch   c6deb0ab791e2364a4055fbe568803ab

round[ 7].istart   cd54c7283864c0c55d4c727e90c9a465

round[ 7].is_box   80fd31ee768c1f078d5d1e8a96121dbc

round[ 7].is_row   80121e0776fd1d8a8d8c31bc965d1fee

round[ 7].im_col   4ee1ddf9301d6352c9ad769ef8d20515

round[ 7].ik_sch   dd1b7cdaf28d5c158a49ab1dbbc497cb

round[ 8].istart   93faa123c2903f4743e4dd83431692de

round[ 8].is_box   2214f132a896251664aec94164ff749c

round[ 8].is_row   22ffc916a81474416496f19c64ae2532

round[ 8].im_col   1008ffe53b36ee6af27b42549b8a7bb7

round[ 8].ik_sch   78c4f708318d3cd69655b701bfc093cf

round[ 9].istart   68cc08ed0abbd2bc642ef555244ae878

round[ 9].is_box   f727bf53a3fe7f788cc377eda65cc8c1

round[ 9].is_row   f75c7778a327c8ed8cfebfc1a6c37f53

round[ 9].im_col   7f69ac1ed939ebaac8ece3cb12e159e3

round[ 9].ik_sch   60dcef10299524ce62dbef152f9620cf

round[10].istart   1fb5430ef0accf64aa370cde3d77792c

round[10].is_box   cbd264d717aa5f8c62b2819c8b02af42

round[10].is_row   cb02818c17d2af9c62aa64428bb25fd7

round[10].im_col   cfaf16b2570c18b52e7fef50cab267ae

round[10].ik_sch   4b4ecbdb4d4dcfda5752d7c74949cbde

round[11].istart   84e1dd691a41d76f792d389783fbac70

round[11].is_box   4fe0c9e443f80d06affa76854163aad0

round[11].is_row   4f63760643e0aa85aff8c9d041fa0de4

round[11].im_col   794cf891177bfd1d8a327086f3831b39

round[11].ik_sch   1a1f181d1e1b1c194742c7d74949cbde

round[12].istart   6353e08c0960e104cd70b751bacad0e7

round[12].is_box   0050a0f04090e03080d02070c01060b0

round[12].is_row   00102030405060708090a0b0c0d0e0f0

round[12].ik_sch   000102030405060708090a0b0c0d0e0f

round[12].ioutput  00112233445566778899aabbccddeeff

C.3 AES-256 (Nk=8, Nr=14)

PLAINTEXT:        00112233445566778899aabbccddeeff

KEY:              000102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f

CIPHER (ENCRYPT):

round[ 0].input   00112233445566778899aabbccddeeff

round[ 0].k_sch   000102030405060708090a0b0c0d0e0f

round[ 1].start   00102030405060708090a0b0c0d0e0f0

round[ 1].s_box   63cab7040953d051cd60e0e7ba70e18c

round[ 1].s_row   6353e08c0960e104cd70b751bacad0e7

round[ 1].m_col   5f72641557f5bc92f7be3b291db9f91a

round[ 1].k_sch   101112131415161718191a1b1c1d1e1f

round[ 2].start   4f63760643e0aa85efa7213201a4e705

round[ 2].s_box   84fb386f1ae1ac97df5cfd237c49946b

round[ 2].s_row   84e1fd6b1a5c946fdf4938977cfbac23

round[ 2].m_col   bd2a395d2b6ac438d192443e615da195

round[ 2].k_sch   a573c29fa176c498a97fce93a572c09c

round[ 3].start   1859fbc28a1c00a078ed8aadc42f6109

round[ 3].s_box   adcb0f257e9c63e0bc557e951c15ef01

round[ 3].s_row   ad9c7e017e55ef25bc150fe01ccb6395

round[ 3].m_col   810dce0cc9db8172b3678c1e88a1b5bd

round[ 3].k_sch   1651a8cd0244beda1a5da4c10640bade

round[ 4].start   975c66c1cb9f3fa8a93a28df8ee10f63

round[ 4].s_box   884a33781fdb75c2d380349e19f876fb

round[ 4].s_row   88db34fb1f807678d3f833c2194a759e

round[ 4].m_col   b2822d81abe6fb275faf103a078c0033

round[ 4].k_sch   ae87dff00ff11b68a68ed5fb03fc1567

round[ 5].start   1c05f271a417e04ff921c5c104701554

round[ 5].s_box   9c6b89a349f0e18499fda678f2515920

round[ 5].s_row   9cf0a62049fd59a399518984f26be178

round[ 5].m_col   aeb65ba974e0f822d73f567bdb64c877

round[ 5].k_sch   6de1f1486fa54f9275f8eb5373b8518d

round[ 6].start   c357aae11b45b7b0a2c7bd28a8dc99fa

round[ 6].s_box   2e5bacf8af6ea9e73ac67a34c286ee2d

round[ 6].s_row   2e6e7a2dafc6eef83a86ace7c25ba934

round[ 6].m_col   b951c33c02e9bd29ae25cdb1efa08cc7

round[ 6].k_sch   c656827fc9a799176f294cec6cd5598b

round[ 7].start   7f074143cb4e243ec10c815d8375d54c

round[ 7].s_box   d2c5831a1f2f36b278fe0c4cec9d0329

round[ 7].s_row   d22f0c291ffe031a789d83b2ecc5364c

round[ 7].m_col   ebb19e1c3ee7c9e87d7535e9ed6b9144

round[ 7].k_sch   3de23a75524775e727bf9eb45407cf39

round[ 8].start   d653a4696ca0bc0f5acaab5db96c5e7d

round[ 8].s_box   f6ed49f950e06576be74624c565058ff

round[ 8].s_row   f6e062ff507458f9be50497656ed654c

round[ 8].m_col   5174c8669da98435a8b3e62ca974a5ea

round[ 8].k_sch   0bdc905fc27b0948ad5245a4c1871c2f

round[ 9].start   5aa858395fd28d7d05e1a38868f3b9c5

round[ 9].s_box   bec26a12cfb55dff6bf80ac4450d56a6

round[ 9].s_row   beb50aa6cff856126b0d6aff45c25dc4

round[ 9].m_col   0f77ee31d2ccadc05430a83f4ef96ac3

round[ 9].k_sch   45f5a66017b2d387300d4d33640a820a

round[10].start   4a824851c57e7e47643de50c2af3e8c9

round[10].s_box   d61352d1a6f3f3a04327d9fee50d9bdd

round[10].s_row   d6f3d9dda6279bd1430d52a0e513f3fe

round[10].m_col   bd86f0ea748fc4f4630f11c1e9331233

round[10].k_sch   7ccff71cbeb4fe5413e6bbf0d261a7df

round[11].start   c14907f6ca3b3aa070e9aa313b52b5ec

round[11].s_box   783bc54274e280e0511eacc7e200d5ce

round[11].s_row   78e2acce741ed5425100c5e0e23b80c7

round[11].m_col   af8690415d6e1dd387e5fbedd5c89013

round[11].k_sch   f01afafee7a82979d7a5644ab3afe640

round[12].start   5f9c6abfbac634aa50409fa766677653

round[12].s_box   cfde0208f4b418ac5309db5c338538ed

round[12].s_row   cfb4dbedf4093808538502ac33de185c

round[12].m_col   7427fae4d8a695269ce83d315be0392b

round[12].k_sch   2541fe719bf500258813bbd55a721c0a

round[13].start   516604954353950314fb86e401922521

round[13].s_box   d133f22a1aed2a7bfa0f44697c4f3ffd

round[13].s_row   d1ed44fd1a0f3f2afa4ff27b7c332a69

round[13].m_col   2c21a820306f154ab712c75eee0da04f

round[13].k_sch   4e5a6699a9f24fe07e572baacdf8cdea

round[14].start   627bceb9999d5aaac945ecf423f56da5

round[14].s_box   aa218b56ee5ebeacdd6ecebf26e63c06

round[14].s_row   aa5ece06ee6e3c56dde68bac2621bebf

round[14].k_sch   24fc79ccbf0979e9371ac23c6d68de36

round[14].output  8ea2b7ca516745bfeafc49904b496089

INVERSE CIPHER (DECRYPT):

round[ 0].iinput   8ea2b7ca516745bfeafc49904b496089

round[ 0].ik_sch   24fc79ccbf0979e9371ac23c6d68de36

round[ 1].istart   aa5ece06ee6e3c56dde68bac2621bebf

round[ 1].is_row   aa218b56ee5ebeacdd6ecebf26e63c06

round[ 1].is_box   627bceb9999d5aaac945ecf423f56da5

round[ 1].ik_sch   4e5a6699a9f24fe07e572baacdf8cdea

round[ 1].ik_add   2c21a820306f154ab712c75eee0da04f

round[ 2].istart   d1ed44fd1a0f3f2afa4ff27b7c332a69

round[ 2].is_row   d133f22a1aed2a7bfa0f44697c4f3ffd

round[ 2].is_box   516604954353950314fb86e401922521

round[ 2].ik_sch   2541fe719bf500258813bbd55a721c0a

round[ 2].ik_add   7427fae4d8a695269ce83d315be0392b

round[ 3].istart   cfb4dbedf4093808538502ac33de185c

round[ 3].is_row   cfde0208f4b418ac5309db5c338538ed

round[ 3].is_box   5f9c6abfbac634aa50409fa766677653

round[ 3].ik_sch   f01afafee7a82979d7a5644ab3afe640

round[ 3].ik_add   af8690415d6e1dd387e5fbedd5c89013

round[ 4].istart   78e2acce741ed5425100c5e0e23b80c7

round[ 4].is_row   783bc54274e280e0511eacc7e200d5ce

round[ 4].is_box   c14907f6ca3b3aa070e9aa313b52b5ec

round[ 4].ik_sch   7ccff71cbeb4fe5413e6bbf0d261a7df

round[ 4].ik_add   bd86f0ea748fc4f4630f11c1e9331233

round[ 5].istart   d6f3d9dda6279bd1430d52a0e513f3fe

round[ 5].is_row   d61352d1a6f3f3a04327d9fee50d9bdd

round[ 5].is_box   4a824851c57e7e47643de50c2af3e8c9

round[ 5].ik_sch   45f5a66017b2d387300d4d33640a820a

round[ 5].ik_add   0f77ee31d2ccadc05430a83f4ef96ac3

round[ 6].istart   beb50aa6cff856126b0d6aff45c25dc4

round[ 6].is_row   bec26a12cfb55dff6bf80ac4450d56a6

round[ 6].is_box   5aa858395fd28d7d05e1a38868f3b9c5

round[ 6].ik_sch   0bdc905fc27b0948ad5245a4c1871c2f

round[ 6].ik_add   5174c8669da98435a8b3e62ca974a5ea

round[ 7].istart   f6e062ff507458f9be50497656ed654c

round[ 7].is_row   f6ed49f950e06576be74624c565058ff

round[ 7].is_box   d653a4696ca0bc0f5acaab5db96c5e7d

round[ 7].ik_sch   3de23a75524775e727bf9eb45407cf39

round[ 7].ik_add   ebb19e1c3ee7c9e87d7535e9ed6b9144

round[ 8].istart   d22f0c291ffe031a789d83b2ecc5364c

round[ 8].is_row   d2c5831a1f2f36b278fe0c4cec9d0329

round[ 8].is_box   7f074143cb4e243ec10c815d8375d54c

round[ 8].ik_sch   c656827fc9a799176f294cec6cd5598b

round[ 8].ik_add   b951c33c02e9bd29ae25cdb1efa08cc7

round[ 9].istart   2e6e7a2dafc6eef83a86ace7c25ba934

round[ 9].is_row   2e5bacf8af6ea9e73ac67a34c286ee2d

round[ 9].is_box   c357aae11b45b7b0a2c7bd28a8dc99fa

round[ 9].ik_sch   6de1f1486fa54f9275f8eb5373b8518d

round[ 9].ik_add   aeb65ba974e0f822d73f567bdb64c877

round[10].istart   9cf0a62049fd59a399518984f26be178

round[10].is_row   9c6b89a349f0e18499fda678f2515920

round[10].is_box   1c05f271a417e04ff921c5c104701554

round[10].ik_sch   ae87dff00ff11b68a68ed5fb03fc1567

round[10].ik_add   b2822d81abe6fb275faf103a078c0033

round[11].istart   88db34fb1f807678d3f833c2194a759e

round[11].is_row   884a33781fdb75c2d380349e19f876fb

round[11].is_box   975c66c1cb9f3fa8a93a28df8ee10f63

round[11].ik_sch   1651a8cd0244beda1a5da4c10640bade

round[11].ik_add   810dce0cc9db8172b3678c1e88a1b5bd

round[12].istart   ad9c7e017e55ef25bc150fe01ccb6395

round[12].is_row   adcb0f257e9c63e0bc557e951c15ef01

round[12].is_box   1859fbc28a1c00a078ed8aadc42f6109

round[12].ik_sch   a573c29fa176c498a97fce93a572c09c

round[12].ik_add   bd2a395d2b6ac438d192443e615da195

round[13].istart   84e1fd6b1a5c946fdf4938977cfbac23

round[13].is_row   84fb386f1ae1ac97df5cfd237c49946b

round[13].is_box   4f63760643e0aa85efa7213201a4e705

round[13].ik_sch   101112131415161718191a1b1c1d1e1f

round[13].ik_add   5f72641557f5bc92f7be3b291db9f91a

round[14].istart   6353e08c0960e104cd70b751bacad0e7

round[14].is_row   63cab7040953d051cd60e0e7ba70e18c

round[14].is_box   00102030405060708090a0b0c0d0e0f0

round[14].ik_sch   000102030405060708090a0b0c0d0e0f

round[14].ioutput  00112233445566778899aabbccddeeff

EQUIVALENT INVERSE CIPHER (DECRYPT):

round[ 0].iinput   8ea2b7ca516745bfeafc49904b496089

round[ 0].ik_sch   24fc79ccbf0979e9371ac23c6d68de36

round[ 1].istart   aa5ece06ee6e3c56dde68bac2621bebf

round[ 1].is_box   629deca599456db9c9f5ceaa237b5af4

round[ 1].is_row   627bceb9999d5aaac945ecf423f56da5

round[ 1].im_col   e51c9502a5c1950506a61024596b2b07

round[ 1].ik_sch   34f1d1ffbfceaa2ffce9e25f2558016e

round[ 2].istart   d1ed44fd1a0f3f2afa4ff27b7c332a69

round[ 2].is_box   5153862143fb259514920403016695e4

round[ 2].is_row   516604954353950314fb86e401922521

round[ 2].im_col   91a29306cc450d0226f4b5eaef5efed8

round[ 2].ik_sch   5e1648eb384c350a7571b746dc80e684

round[ 3].istart   cfb4dbedf4093808538502ac33de185c

round[ 3].is_box   5fc69f53ba4076bf50676aaa669c34a7

round[ 3].is_row   5f9c6abfbac634aa50409fa766677653

round[ 3].im_col   b041a94eff21ae9212278d903b8a63f6

round[ 3].ik_sch   c8a305808b3f7bd043274870d9b1e331

round[ 4].istart   78e2acce741ed5425100c5e0e23b80c7

round[ 4].is_box   c13baaeccae9b5f6705207a03b493a31

round[ 4].is_row   c14907f6ca3b3aa070e9aa313b52b5ec

round[ 4].im_col   638357cec07de6300e30d0ec4ce2a23c

round[ 4].ik_sch   b5708e13665a7de14d3d824ca9f151c2

round[ 5].istart   d6f3d9dda6279bd1430d52a0e513f3fe

round[ 5].is_box   4a7ee5c9c53de85164f348472a827e0c

round[ 5].is_row   4a824851c57e7e47643de50c2af3e8c9

round[ 5].im_col   ca6f71058c642842a315595fdf54f685

round[ 5].ik_sch   74da7ba3439c7e50c81833a09a96ab41

round[ 6].istart   beb50aa6cff856126b0d6aff45c25dc4

round[ 6].is_box   5ad2a3c55fe1b93905f3587d68a88d88

round[ 6].is_row   5aa858395fd28d7d05e1a38868f3b9c5

round[ 6].im_col   ca46f5ea835eab0b9537b6dbb221b6c2

round[ 6].ik_sch   3ca69715d32af3f22b67ffade4ccd38e

round[ 7].istart   f6e062ff507458f9be50497656ed654c

round[ 7].is_box   d6a0ab7d6cca5e695a6ca40fb953bc5d

round[ 7].is_row   d653a4696ca0bc0f5acaab5db96c5e7d

round[ 7].im_col   2a70c8da28b806e9f319ce42be4baead

round[ 7].ik_sch   f85fc4f3374605f38b844df0528e98e1

round[ 8].istart   d22f0c291ffe031a789d83b2ecc5364c

round[ 8].is_box   7f4e814ccb0cd543c175413e8307245d

round[ 8].is_row   7f074143cb4e243ec10c815d8375d54c

round[ 8].im_col   f0073ab7404a8a1fc2cba0b80df08517

round[ 8].ik_sch   de69409aef8c64e7f84d0c5fcfab2c23

round[ 9].istart   2e6e7a2dafc6eef83a86ace7c25ba934

round[ 9].is_box   c345bdfa1bc799e1a2dcaab0a857b728

round[ 9].is_row   c357aae11b45b7b0a2c7bd28a8dc99fa

round[ 9].im_col   3225fe3686e498a32593c1872b613469

round[ 9].ik_sch   aed55816cf19c100bcc24803d90ad511

round[10].istart   9cf0a62049fd59a399518984f26be178

round[10].is_box   1c17c554a4211571f970f24f0405e0c1

round[10].is_row   1c05f271a417e04ff921c5c104701554

round[10].im_col   9d1d5c462e655205c4395b7a2eac55e2

round[10].ik_sch   15c668bd31e5247d17c168b837e6207c

round[11].istart   88db34fb1f807678d3f833c2194a759e

round[11].is_box   979f2863cb3a0fc1a9e166a88e5c3fdf

round[11].is_row   975c66c1cb9f3fa8a93a28df8ee10f63

round[11].im_col   d24bfb0e1f997633cfce86e37903fe87

round[11].ik_sch   7fd7850f61cc991673db890365c89d12

round[12].istart   ad9c7e017e55ef25bc150fe01ccb6395

round[12].is_box   181c8a098aed61c2782ffba0c45900ad

round[12].is_row   1859fbc28a1c00a078ed8aadc42f6109

round[12].im_col   aec9bda23e7fd8aff96d74525cdce4e7

round[12].ik_sch   2a2840c924234cc026244cc5202748c4

round[13].istart   84e1fd6b1a5c946fdf4938977cfbac23

round[13].is_box   4fe0210543a7e706efa476850163aa32

round[13].is_row   4f63760643e0aa85efa7213201a4e705

round[13].im_col   794cf891177bfd1ddf67a744acd9c4f6

round[13].ik_sch   1a1f181d1e1b1c191217101516131411

round[14].istart   6353e08c0960e104cd70b751bacad0e7

round[14].is_box   0050a0f04090e03080d02070c01060b0

round[14].is_row   00102030405060708090a0b0c0d0e0f0

round[14].ik_sch   000102030405060708090a0b0c0d0e0f

round[14].ioutput  00112233445566778899aabbccddeeff

Appendix D - References

[1] AES page available via http://www.nist.gov/CryptoToolkit.4

[2] Computer Security Objects Register (CSOR): http://csrc.nist.gov/csor/.

[3] J. Daemen and V. Rijmen, AES Proposal: Rijndael, AES Algorithm Submission, September 3, 1999, available at [1].

[4] J. Daemen and V. Rijmen, The block cipher Rijndael, Smart Card research and Applications, LNCS 1820, Springer-Verlag, pp. 288-296.

[5] B. GladmanÆs AES related home page http://fp.gladman.plus.com/cryptography_technology/.

[6] A. Lee, NIST Special Publication 800-21, Guideline for Implementing Cryptography in the Federal Government, National Institute of Standards and Technology, November 1999.

[7] A. Menezes, P. van Oorschot, and S. Vanstone, Handbook of Applied Cryptography, CRC Press, New York, 1997, p. 81-83.

[8] J. Nechvatal, et. al., Report on the Development of the Advanced Encryption Standard (AES), National Institute of Standards and Technology, October 2, 2000, available at [1].

____________________

4 A complete set of documentation from the AES development effort û including announcements, public comments, analysis papers, conference proceedings, etc. û is available from http://csrc.nist.gov/encryption/aes/.

Transcription and HTML by Cryptome.

Copyright ⌐ 2006, KinoCode, Inc.